An introduction to systems biology modelling¶
Introduction¶
Welcome to the introductory systems biology computer exercise! This exercise is a simplified version of a typical workflow. You will be introduced to hypotheses of a biological system, and will then formulate models of these to describe experimental data. Then, you will test the different hypothesis to see if you can reject any of them using experimental data, and finally make predictions with the models.
This version of the exercise is implemented as a Python version using the SciPy toolbox, running in an iPython notebook. The notebook can either be run online in Google Colab, or downloaded and run locally.
Note: if running in Google Colab, the first thing you should do is to save a copy of the notebook. To do this, press File > Save a copy in Drive. Also be aware that files created (e.g. for results later) are NOT saved when exiting the session, therefore always download backups of results. The notebook itself is saved between sessions.
About Python and notebooks¶
In a Python notebook, you can create either text or code cells. Text cells contain information like this, formatted using Markdown. Text cells can be edited by clicking twice in the box, and can be exited by clicking outside the text cell or by pressing save (differs based on notebook handler). Code cells contain actual code that can be run, typically by pressing a play button located on the top left of a code-cell when the mouse is kept over the cell (again it might differ a bit based on notebook handler). If running on Google Colab, note that the first time you run a cell (and after being idle for a longer time) you will be connected to server that runs the code, thus the first you run a cell, you might have to wait a short while.
One final note, is that Python uses so called "zero-based indexing", which means that the first position in for example lists have index 0, and the second position have index 1 and so on.
Now, you are ready to start the main tasks!
Importing necessary packages¶
Python is structured in such a way that only a core set of functions are available in the default setting. Instead, useful functions are stored in optional packages. To use the functions in these packages, we need to explicitly import the packages.
import sys
import json
import csv
import random
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
from scipy.stats import chi2
from scipy.optimize import dual_annealing
Model formulation and the experimental data¶
Getting to know the experimental data¶
During the exercises you will take on the role of a system biologist working in collaboration with an experimental group. The experimental group have collected data for an experimental system. You can read more of the background by clicking on the expandable Background section on the next line.
Background (click me)
The experimental group is focusing on the cellular response to growth factors, like the epidermal growth factor (EGF), and their role in cancer. The group have a particular interest in the phosphorylation of the receptor tyrosine kinase EGFR in response to EGF and therefore perform an experiment to elucidate the role of EGFR. In the experiment, they stimulate a cancer cell line with EGFR and use an antibody to measure the tyrosine phosphorylation at site 992, which is known to be involved in downstream growth signaling. The data from these experiments show an interesting dynamic behavior with a fast increase in phosphorylation followed by a decrease down to a steady-state level which is higher than before stimulation (Figure 1).
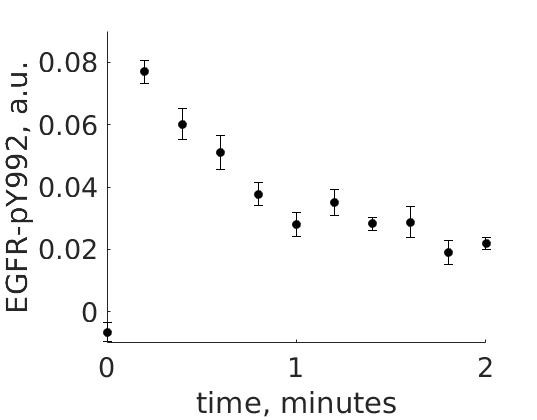
Figure 1: The experimental data. A cancer cell line is stimulated with EGF at time point 0, and the response at EGFR-pY992 is measured
The experimental group does not know the underlying mechanisms that give rise to this dynamic behavior. However, they have two different ideas of possible mechanisms, which we will formulate as hypotheses below. The first idea is that there is a negative feedback transmitted from EGFR to a downstream signaling molecule that is involved in dephosphorylation of EGFR. The second idea is that a downstream signaling molecule is secreted to the surrounding medium and there catalyzes breakdown of EGF, which also would reduce the phosphorylation of EGFR. The experimental group would like to know if any of these ideas agree with their data, and if so, how to design experiments to find out which is the more likely idea.
To generalize this problem, we use the following notation:
EGF – Stimulation (S)
EGFR – Receptor (R)
The next step now is to set up the experimental data.
Defining the data¶
Typically, datasets are saved in files and loaded into the analysis script. In this case, we have inserted the values corresponding to the experimental data here: time points, mean values and standard deviations of the mean (SEM).
The data is structured in what is called a dictionary (dict). In short, a dictionary contains a pair of keys and values. Below, we print the keys of the dict and the values of one key (time).
data = {} # create an empty dictionary
data['time'] = [0.0, 0.2, 0.4, 0.6, 0.8, 1.0, 1.2, 1.4, 1.6, 1.8, 2.0]
data['mean'] =[-0.0065112, 0.076965, 0.060161, 0.050973, 0.03768, 0.027949, 0.034981, 0.028261, 0.028708, 0.019014, 0.021887]
data['SEM'] = [0.0027889, 0.0035225, 0.0045911, 0.0051342, 0.0034731, 0.0036044, 0.0038831, 0.0019989, 0.0047651, 0.0036907, 0.0018121]
print('All content of data:')
print(data)
print('\nKeys in the data:')
print(data.keys())
print('\nThe content of the "time" key:')
print(data["time"])
Plotting the data¶
Now that we have loaded the data, we should visualize it.
We do this by plotting the data using the package matplotlib and pyplot. In practice, we have shortened the name of matplotlib.pyplot package to plt when we imported the package earlier (import matplotlib.pyplot as plt). We plot the data using the errorbar function, and set the color to black, and the marker symbol to "o".
To make the code reusable for later, we wrap the plotting inside a function plot_data which takes data as input. Finally, we plot the data and show the figure using the plot function
def plot_data(data):
plt.errorbar(data['time'], data['mean'], data['SEM'], linestyle='None', marker='o', color='black', capsize=5)
plt.xlabel('Time (min)')
plt.ylabel('Phosphorylation (a.u.)')
plot_data(data)
Define, simulate and plot a first model¶
The experimentalists have an idea of how they think the biological system they have studied works. We will now create a mathematical representation of this hypothesis.
The hypothesis (click me)
To go from the first idea to formulate a hypothesis, we include what we know from the biological system:
- A receptor (R) is phosphorylated (Rp) in response to an activation (A)
- A downstream signaling molecule (S) is also phosphorylated, as an effect of the phosphorylation of the receptor
- The active downstream signaling molecule (Sp) is involved in the dephosphorylation of the receptor
- Phosphorylated/active molecules can return to inactive states without stimuli
Based on the behavior in the data, and the prior knowledge of the system, the experimentalists have constructed the hypothesis depicted in the figure below.
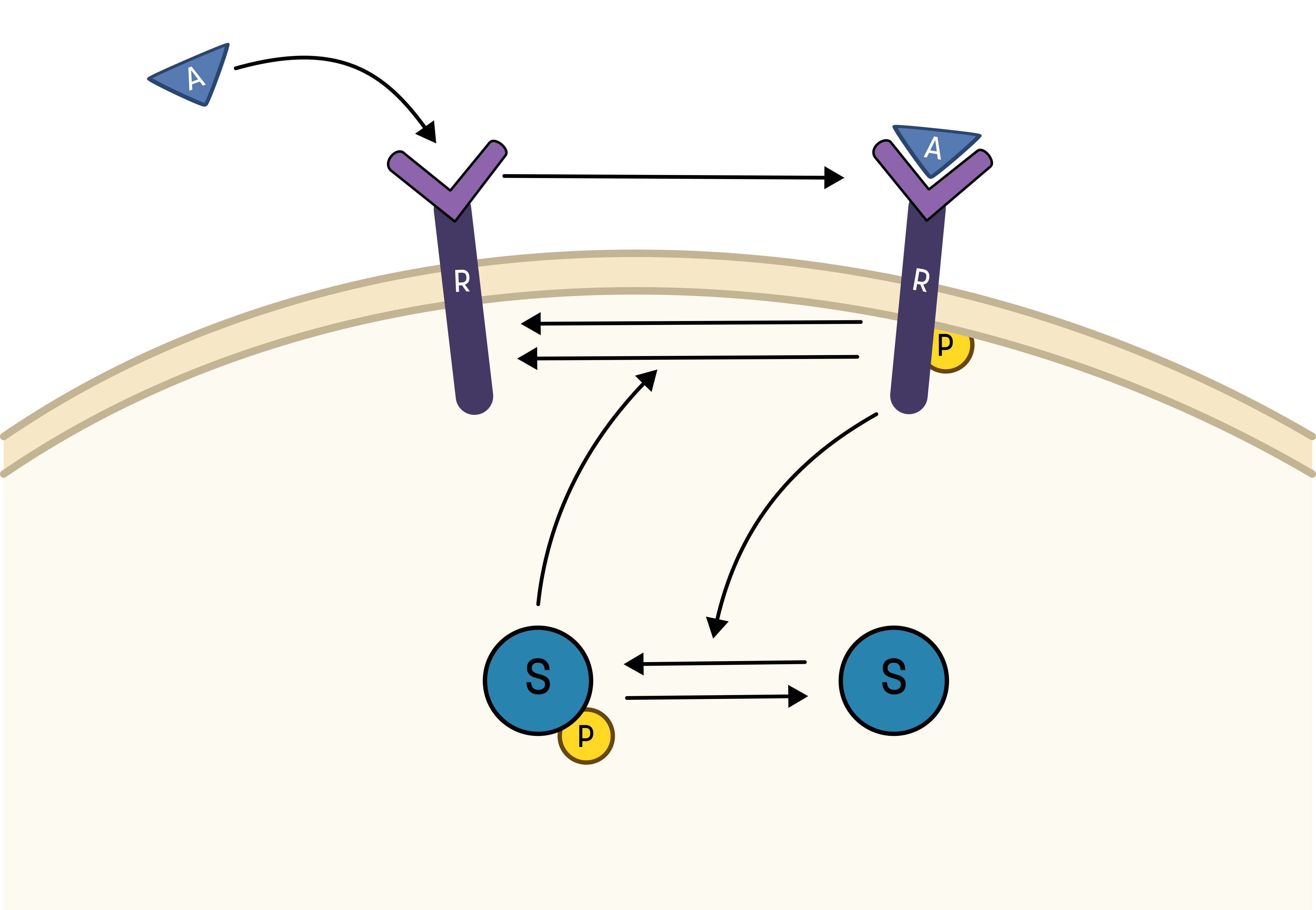
From this hypothesis, we can draw an interaction graph, along with a description of the reactions.
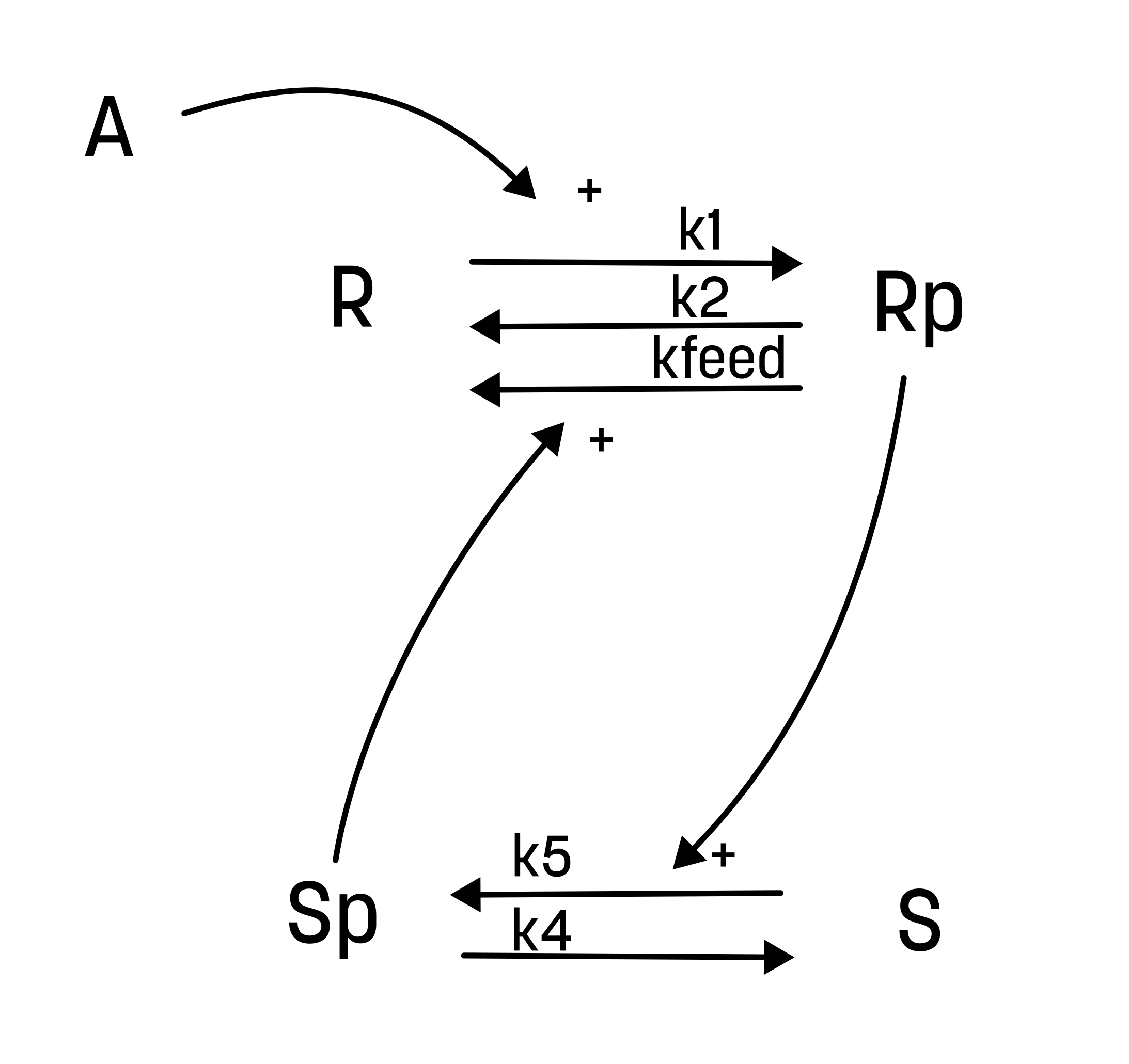
The reactions are as follows:
- Reaction 1 is the phosphorylation of the receptor (R). It depends on the state R, with the input A and the parameter k1.
- Reaction 2 is the basal dephosphorylation of Rp to R. It depends on the state Rp with the parameter k2.
- Reaction 3 is the feedback-induced dephosphorylation of Rp to R exerted by Sp. This reaction depends on the states Rp and Sp with the parameter kfeed.
- Reaction 4 is the basal dephosphorylation of Sp to S. It depends on the state Sp with the parameter k4.
- Reaction 5 is the phosphorylation of S to Sp. This phosphorylation is regulated by Rp. The reaction depends on the states S and Rp, with the parameter k5.
Rp is what have been measured experimentally.
The experimentalist have guessed the values of both the initial conditions and the parameter values
| Initial values | Parameter values |
|---|---|
| R(0) = 1 | k1 = 1 |
| Rp(0) = 0 | k2 = 0.0001 |
| S(0) = 1 | kfeed = 1000000 |
| Sp(0) = 0 | k4 = 1 |
| k5 = 0.01 |
The next step now is to implement the hypothesis as a model, and then simulate the model. To get started quicker, we have implemented the first part of the hypothesis (R and Rp) for you (without reaction 3). Call this extended model M1. Now, implement the rest of the equations for M1.
def M1(state,t, param):
# Define the stimulation
if t >= 0:
A = 1
# Update below with your equations for hypothesis 1.
# Define the states
R = state[0]
Rp = state[1]
# Define the parameter values
k1 = param[0]
k2 = param[1]
# Define the reactions
r1 = R*A*k1
r2 = Rp*k2
# Define the ODEs
ddt_R = -r1
ddt_Rp = -r2
ddt_S = 0
ddt_Sp = 0
return[ddt_R, ddt_Rp, ddt_S, ddt_Sp]
Plotting the model simulation agreement with data¶
Now we want to compare how well the model agree with the experimental data.
First we create a function that can simulate and plot the model. To simulate the model, we need to give the parameter values param, initial conditions ic, and the time points t. We also provide two optional keyword arguments of which state to plot state_to_plot and the color of the plotted line line_color.
def plot_simulation(model, param, ic, t, state_to_plot=1, line_color='b'):
sim = odeint(model, ic, t, (param,)) # Simulate the model for the initial parameters in the model file
plt.plot(t, sim[:,state_to_plot], color=line_color) # The data corresponds to Rp which is the second state
We use the functions for plotting the data and the simulation to create a plot that shows how well the model simulation agrees with the data. Note that the agreement is (probably) not very good.
Importantly, we also simulate the model with a high time resolution (between 0 and 2, with a step size of 0.01: t_hr = np.arange(0, 2, 0.01)). We do this to check the stability of the model, and to make sure that we are not accidentally plotting noise.
param0_M1 = [1, 0.0001, 1000000, 1, 0.01] #[k1 = 1, k2 = 0.0001, kfeed = 1000000, k4 = 1, k5 = 0.01]
ic_M1 = [1, 0, 1, 0] #[R(0) = 1, Rp(0) = 0, S(0) = 1, Sp(0) = 0]
t_hr = np.arange(0, 2, 0.01)
plot_simulation(M1, param0_M1, ic_M1, t_hr, state_to_plot=1)
plot_data(data)
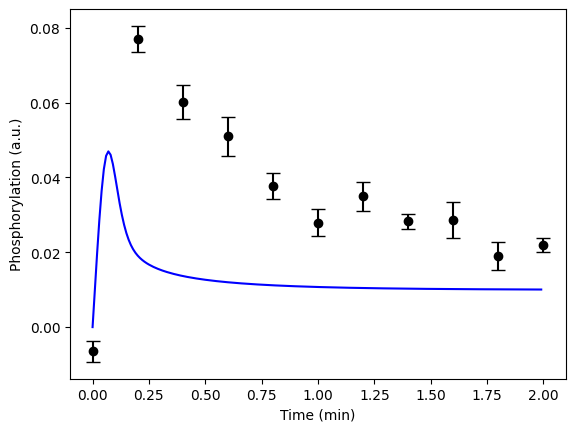
(spoilers) Self-check: Have I implemented the model correctly?
If you have done everything correctly, you should have a figure which looks like this for the first hypothesis with the given values:
Improving the agreement manually (if there is time)¶
If you have extra time, try to find a combination of parameter values that improves the agreement to data.
param_manual_M1 = [1, 0.0001, 1000000, 1, 0.01] # = [k1, k2, kfeed, k4, k5]
plot_simulation(M1, param_manual_M1, ic_M1, t_hr, state_to_plot=1)
plot_data(data)
Checkpoint and reflection¶
This marks the end of the first section of the exercise. Show your figure which shows how well the model agrees with the data.
Questions to reflect over
- Why do we simulate with a time-resolution higher than the resolution of the data points?
- When is the agreement good enough?
- What could be possible reasons why not all states of the model are measured experimentally?
- (optional) Was it easy finding a better agreement? What if it was a more complex model, or if there were more data series?
Evaluating and improving the agreement to data¶
Clearly, the agreement to data (for the given parameter set) is not perfect, but it is still better than the first overly simple model. However, a question now arises: how good does the model simulation agree with data?
We typically evaluate the model agreement using a sum or squared residuals, weighted with the uncertainty of the data, often referred to as the cost of the model agreement.
$$v\left(\theta\right)=\ \sum_{\forall t}\left(\frac{{y_t -\ {\hat{y}}_t\left(\theta\right)}}{{SEM}_t}\right)^2$$where $v(\theta)$ is the cost given a set of parameters $\theta$, $y_t$ and $SEM_t$ is experimental data (mean and SEM) at time $t$, and ${\hat{y}}_t$ is model simulation at time $t$. Here, $y_t-\ {\hat{y}}_t\left(\theta\right)$, is commonly referred to as residuals, and represent the difference between the simulation and the data in each timepoint.
The cost function is defined in the code cell below.
def fcost(param, model, ic, data):
t = data["time"]
sim = odeint(model, ic, t, (param,))
ysim = sim[:,1]
y = np.array(data["mean"])
sem = np.array(data["SEM"])
cost = np.sum(np.square((y - ysim) / sem))
return cost
param0_M1 = [1, 0.0001, 1000000, 1, 0.01] # = [k1, k2, kfeed, k4, k5]
ic_M1 = [1, 0, 1, 0] # = [R(0), Rp(0), S(0), Sp(0)]
cost_M1 = fcost(param0_M1, M1, ic_M1, data)
print(f"Cost of the M1 model: {cost_M1}")
(spoilers) Self-check: What should the cost for the initial parameter set be if the model is implemented correctly?
The cost for the initial parameter set should be approximately 701
Evaluating if the agreement is good enough¶
To get a quantifiable statistical measurement for if the agreement is good enough, or if the model/hypothesis should be rejected, we can use a $\chi^2$-test. We compare if the cost is exceeding the threshold set by the $\chi^2$-statistic. We typically do this using p = 0.05, and setting the degrees of freedom to the number of residuals summed (i.e. the number of data points).
If the cost exceeds the $\chi^2$-limit, we reject the model/hypothesis.
dgf = len(data["mean"])
chi2_limit = chi2.ppf(0.95, dgf) # Here, 0.95 corresponds to 0.05 significance level
print(f"Chi2 limit: {chi2_limit}")
print(f"Cost > limit (rejected?): {cost_M1>chi2_limit}")
Improving the agreement (manually)¶
As suspected, the agreement to the data was too bad, and the model thus had to be rejected. However, that is only true for the current values of the parameters. Perhaps this structure of the model can still explain the data good enough with other parameter values? To determine if the model structure (hypothesis) should be rejected, we must determine if the parameter set with the best agreement to data still results in a too bad agreement. If the best parameter set is too bad, no other parameter set can be good enough, and thus we must reject the model/hypothesis.
Try to change some parameter values to see if you can get a better agreement. It is typically a good idea to change one parameter at a time to see the effect of changing one parameter. If you did this in the previous section, you can reuse those parameter values.
param_guess_M1 = [1, 0.0001, 1000000, 1, 0.01] # Change the values here and try to find a better agreement
# param_guess_M1 = param_manual # If you tried to find a better agreement visually above, you can copy the values here
ic_M1 = [1, 0, 1, 0]
t_hr = np.arange(0, 2, 0.01)
cost = fcost(param_guess_M1, M1, ic_M1, data)
print(f"Cost of the M1 model: {cost}")
dgf = len(data["mean"])
chi2_limit = chi2.ppf(0.95, dgf)
print(f"Chi2 limit: {chi2_limit}")
print(f"Cost > limit (rejected?): {cost>chi2_limit}")
plot_simulation(M1, param_guess_M1, ic_M1, t_hr, state_to_plot=1)
plot_data(data)
Improving the agreement (using optimization methods)¶
As you have probably noticed, estimating the values of the parameters can be a hard and time-consuming work. To our help, we can use optimization methods. There exists many toolboxes and algorithms that can be used for parameter estimation. In this short example, we will use an algorithm called dual annealing from the SciPy toolbox. It is called in the following way: res = dual_annealing(func, bounds, args, x0, callback)
Description of the dual annealing function arguments
func- an objective function (we can use the cost functionfcostdefined earlier),bounds- bounds of the parameter values,args- arguments needed for the objective function, in addition to the parameter values to test (in our case model, initial conditions and data:fcost(param, model, ic, data))x0- a start guess of the parameter values (e.g.param_guess_M1),callback- a "callback" function. The callback function is called at each iteration of the optimization, and can for example be used to print the current solution.
The dual annealing function returns a dictionary (res) with the keys x corresponding to the best found parameter values, and fun which corresponds to the cost for the values of x.
Defining the callback function:¶
This basic callback function prints the result to the output and also saves the current best solution to a temporary file.
def callback_M1(x,f,c):
global niter
if niter%1 == 0:
print(f"Iter: {niter:4d}, obj:{f:3.6f}", file=sys.stdout)
with open("./M1-temp.json",'w') as file:
out = {"f": f, "x": list(x)}
json.dump(out,file)
niter+=1
Running the optimization¶
Now it is time to run the optimization to find better parameter values.
The optimization problem is not guaranteed to give the optimal solution, therefore you might need to restart the optimization a few times (perhaps with different starting guesses) to get a good solution.
Additional notes about optimization and saving/loading parameter values (click me)
Problematic simulations¶
Note that you might sometimes get warnings about odeint issues. If this only rarely happens, it is a numerical issue and nothing to worry about, but if it is the only thing happens, and you get no progress, something is wrong.
Saving/loading parameters¶
After the optimization, the results is saved into a JSON file. Remember, if you run on Google Colab, the files will not be saved when you disconnect from the server. So, if you want to save a parameter set permanently, download the parameter set.
If you later want to load the parameter set you can do that using the code snippet below. Remember to change file_name.json to the right file name. The loaded file will be a dictionary, where the parameter values can be accessed using results['x']
with open('file_name.json','r') as file:
res = json.load(f)
Computational time for different scales of model sizes¶
Optimizing model parameters in larger and more complex models, with additional sets of data, will take a longer time that in this exercise. In a "real" project, it likely takes hours if not days to find the best solution.
bounds_M1 = np.array([(1.0e-6, 1.0e6)]*(len(param_guess_M1)))
args_M1 = (M1, ic_M1, data)
niter = 0
res = dual_annealing(func=fcost, bounds=bounds_M1, args=args_M1, x0=param_guess_M1, callback=callback_M1) # This is the optimization
print(f"\nOptimized parameter values: {res['x']}")
print(f"Optimized cost: {res['fun']}")
print(f"chi2-limit: {chi2_limit}")
print(f"Cost > limit (rejected?): {res['fun']>chi2_limit}")
if res['fun'] < chi2_limit: #Saves the parameter values, if the cost was below the limit.
file_name = f"M1 ({res['fun']:.3f}).json"
with open(file_name,'w') as file:
res['x'] = list(res['x']) #We save the file as a .json file, and for that we have to convert the parameter values that is currently stored as a ndarray into a traditional python list
json.dump(res, file)
(spoilers) Self-check: How good solution should I have found?
You should have found a cost that is less than 18. If not, run the optimization a few more times. If you still do not find it, make sure that your model is implemented correctly.
Now, let's plot the solution you found using the optimization
plot_simulation(M1, res['x'], ic_M1, t_hr, state_to_plot=1)
plot_data(data)
Checkpoint and reflection¶
Show the plot with the best agreement to data, and the cost for the same parameter set. Do you reject the model? Briefly describe the cost function: What are the residuals? Why do we normalize with the squared uncertainty?
If running in Google Colab: remember to save the best solution you have found before exiting the session!
Questions to reflect over
- Why do we want to find the best solution?
- Are we guaranteed to find the best solution?
- Do you reject the first hypothesis?
- If you did not reject the model, how can you test the model further?
Using the model to make predictions¶
If the optimization did not encounter big issues you should have been able to find a solution that passed the $\chi^2$-test. However, it is still possible that we have not found the right model and/or parameter values. For example, since the data have uncertainty it is possible that we have overfitted to uncertain (incorrect) data. An overfitted model would in general be good at explaining the data used for parameter estimation, but might not be good at explaining new data (i.e. making predictions).
For this reason, we do not only want to find the parameter set with the best agreement to data, but rather all parameter sets that agree with the estimation data. Since collecting all sets of parameter values is infeasible from a computational standpoint, we typically try to find the parameter sets that result in the simulations which gives the extreme (maximal/minimal) simulations in each time point.
The best way of finding the extremes is to directly optimize the value by reformulating the optimization problem, or to use Markov-Chain Monte-Carlo (MCMC) methods. Here, we will not do this due to time-constraints, and will instead use a simple (inferior) approach that simply stores a bunch of parameter sets that result in a cost below the threshold of rejection. This gives us a quick approximation of the uncertainty, which is good enough for this exercise. In future projects, you should try to find the maximal uncertainty.
To save all parameters, we need to create a function which both calculates the cost, and stores acceptable parameters. We reuse fcost, and introduce a new variable all_params_M1 to save the acceptable parameter to.
all_params_M1 = [] # Initiate an empty list to store all parameters that are below the chi2 limit
def fcost_uncertainty_M1(param, model, ic, data):
cost = fcost(param, model, ic, data) # Calculate the cost using fcost
# Save the parameter set if the cost is below the limit
if cost < chi2.ppf(0.95, dgf):
all_params_M1.append(param)
return cost
Then we rerun the optimization a couple of times to get some values saved.
niter = 0
res = dual_annealing(func=fcost_uncertainty_M1, bounds=bounds_M1, args=args_M1, x0=param_guess_M1, callback=callback_M1) # This is the optimization
print(f"Number of parameter sets collected: {len(all_params_M1)}") # Prints how many parameter sets that were accepted
Make sure that there are at least 250 saved parameter sets.
You can save the found parameter sets by e.g. saving them to a CSV file. This file can then be loaded if you are returning later.
The code cell below contains code for both saving and loading a set of acceptable parameters for reference.
# Save the accepted parameters to a csv file
with open('all_params_M1.csv', 'w', newline='') as csvfile:
writer = csv.writer(csvfile, delimiter=',')
writer.writerows(all_params_M1)
# load the accepted parameters from the csv file
with open('all_params_M1.csv', newline='') as csvfile:
reader = csv.reader(csvfile, delimiter=',', quoting=csv.QUOTE_NONNUMERIC)
all_params_M1 = list(reader)
Now, we plot the simulation uncertainty.
To save some time, we randomize the order of the saved parameter sets, and only plot the first 200. Obviously this results in an underestimated simulation uncertainty, but the uncertainty should still be sufficient for this exercise. In a real project, one would simulate all collected parameter sets (or sample using the reformulated optimization problem, or MCMC).
random.shuffle(all_params_M1)
for param in all_params_M1[:200]:
plot_simulation(M1, param, ic_M1, t_hr, state_to_plot=1)
plot_data(data)
Testing the model further by making predictions¶
Finally, now that we have estimated the model uncertainty, we can make predictions with uncertainty. A prediction can almost be anything, but in practice it is common to use a different input strength (A in the model), or to change the input after a set time. It is also possible to extend the simulated time beyond the measured time points. Finally, it is also possible to use the simulation in between already measured data points.
In this exercise, we suggest that you change the input strength A to 2 at time point t = 2, and that you simulate 2 additional minutes (to t = 4). Firstly, this requires that we update the model to change the input. We have supplied a template with the updated input strength handling. You should copy your model of hypothesis 1 used above.
def M1_pred(state,t, param):
if t >= 2:
A = 2
elif t >= 0:
A= 1
# Update below with your M1 model.
# Define the states
R = state[0]
Rp = state[1]
# Define the parameter values
k1 = param[0]
k2 = param[1]
# Define the reactions
r1 = R*A*k1
r2 = Rp*k2
# Define the ODEs
ddt_R = -r1
ddt_Rp = -r2
ddt_S = 0
ddt_Sp = 0
return[ddt_R, ddt_Rp, ddt_S, ddt_Sp]
Finally, we need to extend the simulated time vector from ending at t = 2, to ending at t = 4, and then simulate the prediction using the sampled parameter sets.
t_hr_4 = np.arange(0, 4, 0.01)
for param in all_params_M1[:200]:
plot_simulation(M1_pred, param, ic_M1, t_hr_4, state_to_plot=1)
plot_data(data)
The experimentalists have now measured your prediction (of setting A = 2 at t = 2), and are presenting the following additional prediction data to you.
data_pred = {}
data_pred['time'] = [2.25, 2.5, 2.75, 3.0, 3.25, 3.5, 3.75, 4.0]
data_pred['mean'] = [0.130148, 0.070192, 0.059823, 0.038678, 0.034251, 0.032175, 0.029674, 0.026648]
data_pred['SEM'] = [0.022427, 0.012864, 0.009188, 0.008876, 0.008798, 0.008431, 0.008488, 0.008232]
plot_data(data_pred)
Now, plot your prediction, the original data and the new data together. Did your model predict the new data correctly?
t_hr_4 = np.arange(0, 4, 0.01)
for param in all_params_M1[:200]:
plot_simulation(M1_pred, param, ic_M1, t_hr_4, state_to_plot=1)
plot_data(data)
plot_data(data_pred)
Testing an alternative hypothesis¶
As you should see, the first hypothesis did not predict the new data well. Therefore, you have gone back to the biologists with whom you come up with an alternative second hypothesis: that the activator A is not constant and will instead be removed over time. Implement this alternative hypothesis (given below), check if it can explain the original data, and if it can, collect the uncertainty and check if it can predict the new data correctly.
The second hypothesis (click me!)
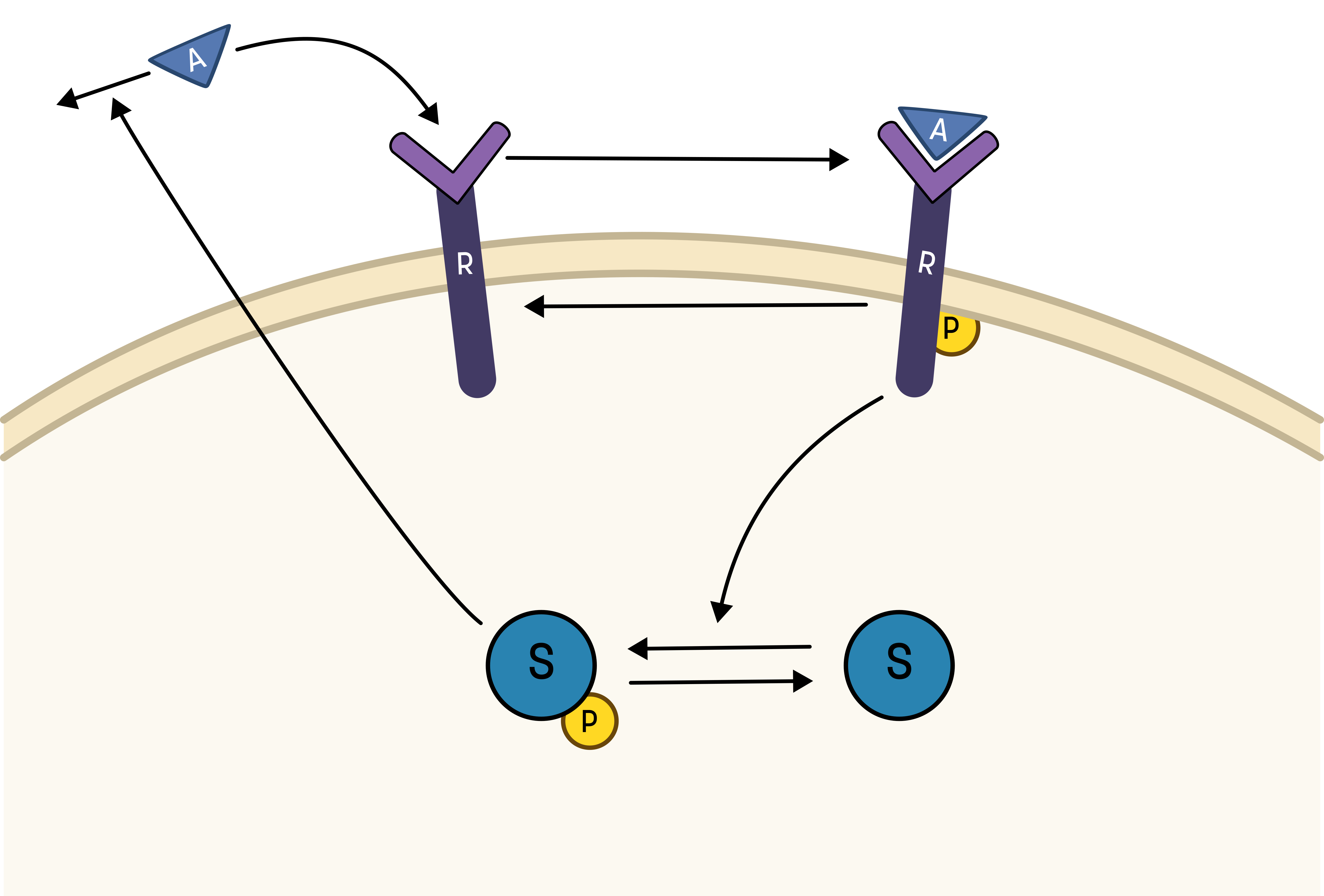
This hypothesis is similar to the first one, but with some modifications:
- The feedback-induced dephosphorylation of Rp (reaction 3 in the first hypothesis) is removed.
- A new feedback-dependent breakdown of the activator A is added. This reaction is dependent on the states Sp and A with a parameter kfeed (same name, but a different mode of action).
These differences yield the following interaction-graph:
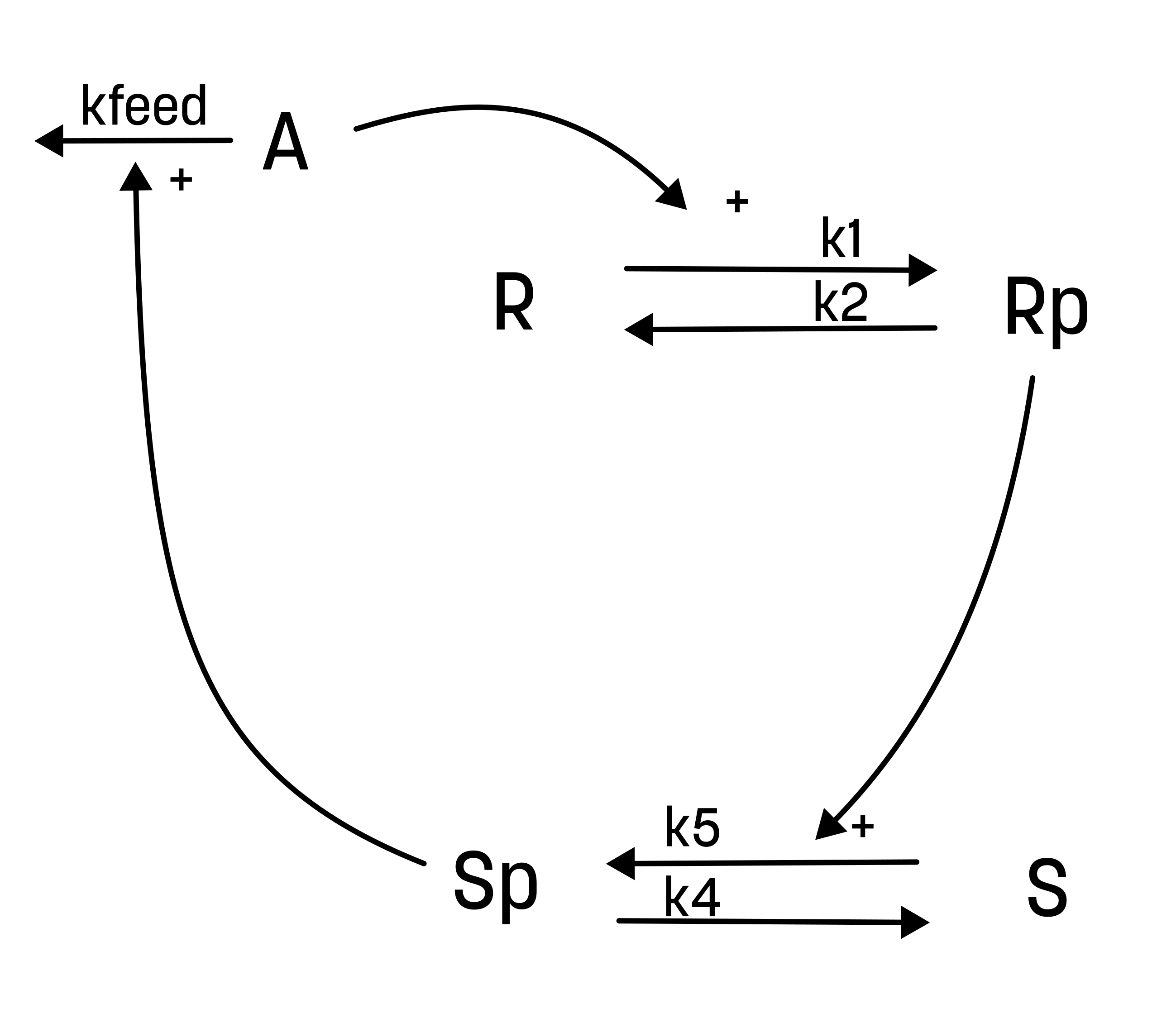
For the alternative hypothesis, the experimentalist have also guessed the values of both the initial conditions and the parameter values.
| Initial values | Parameter values |
|---|---|
| R(0) = 1 | k1 = 5 |
| Rp(0) = 0 | k2 = 20 |
| S(0) = 1 | kfeed = 10 |
| Sp(0) = 0 | k4 = 15 |
| A(0) = 1 | k5 = 30 |
Note that A is now a state and not a constant input.
Start by implementing the new model.
# Implement a model of the second hypothesis here
def M2(state,t, param):
# Update below with your M2 model.
# Define the states
R = state[0]
Rp = state[1]
A = state[4] # A should be the last state in the model for the rest of the code to work properly
# Define the parameter values
k1 = param[0]
k2 = param[1]
# Define the reactions
r1 = R*A*k1
r2 = Rp*k2
# Define the ODEs
ddt_R = -r1
ddt_Rp = -r2
ddt_S = 0
ddt_Sp = 0
ddt_A = 0
return[ddt_R, ddt_Rp, ddt_S, ddt_Sp, ddt_A]
Then test the supplied parameters, and plot the agreement to data.
# Test how well the model fits the original data given the good parameter set (is the model rejected?)
## Calculate the cost of the new model, test with a chi2 test if the model is rejected or not
## Plot the agreement to data
(spoilers) Self-check: How can I know if M2 have been implemented correctly?
The cost for the given parameter set should be 905. If it isn't, you might have incorrect equations, or have placed the states or parameters in the incorrect order. It is also possible that you are simulating with parameter values from the wrong model.
Implement the callback, and create a new function for saving the parameter values
# Implement a new callback, remember to switch the names from M1 to M2
# Setup for estimating the model uncertainty
## Initialize an empty list to store all accepted parameter sets
## Define a new cost function that saves all accepted parameter sets in the list
## Setup bounds and arguments for the optimization
Again, collect the parameter sets by optimizing the parameter values a couple of times
# Run the optimization to gather the uncertainty, remember to run for M2 and to update all input arguments to the optimizer.
Because A is now a state, we cannot set the values based on the time as done in M1_pred. Instead, we need to perform two consecutive simulations, where A is set at the start of each simulation. We do this using the plot_prediction_M2 function defined below.
Note that the time vector should now be split into two parts, t1 and t2, ranging from 0 to 2 and from 2 to 4 respectively.
def plot_prediction_M2(model, param, ic, t1, t2, state_to_plot=1, line_color = 'b'):
sim1 = odeint(model, ic, t1, (param,)) # Simulate the model for the initial parameters in the model file
ic2 = sim1[-1,:] # The initial conditions for the second simulation is the last state of the first simulation
ic2[4] = 2 # The value of A is set to 2 for the second simulation
sim2 = odeint(model, ic2, t2, (param,)) # Simulate the model for the second stimulation
t = np.concatenate((t1,t2)) # Combine the time points from the two simulations
sim = np.concatenate((sim1[:,state_to_plot], sim2[:,state_to_plot])) # Combine the two simulations
plt.plot(t, sim, color=line_color) # The data corresponds to Rp which is the second state
Sample the parameters and plot the prediction with the original data and the new validation data. Does this model agree with the prediction dataset?
# Sample the parameter sets, plot the simulations with uncertainty, and plot the prediction data
Present the results of your predictions for the experimentalists¶
Before going to the final meeting with the experimentalists, you should prepare a figure which contain both of the model predictions and both of the data sets in one single figure, so that you can explain clearly which hypotheses should be rejected and which should be investigated further.
# Sample the parameter sets, plot the simulations with uncertainty for both models, as well as both of the data sets
## Plot model 1
## Plot model 2 (remember to select a different color by changing the line_color argument)
## Plot estimation data
## Plot prediction data
Checkpoint and reflection¶
Present the figure with the prediction with uncertainty from both of the models, and how well they agree with the data. Explain if you should reject any of the models based on this figure.
Questions to reflect over
- Did you reject any of the models?
- What are the strengths of finding core predictions that are different between models potentially describing the same system?
- What is the downside to choosing points where there is an overlap between the models to test experimentally, even if the predictions are certain ("narrow")?
- What would be the outcome if it was impossible (experimentally) to measure between 2 and 3 minutes?
- Is our simulation uncertainty reasonable? Is it over- or underestimated?
- What could be problems related to overestimating the uncertainty? To underestimating the uncertainty?
- What should you do when your model can correctly predict new data?
Summary and final discussion¶
This concludes this introductory exercise to systems biology. In the exercise, you should have learned the basics of implementing and simulating models, testing the models using a $\chi^2$-test, collecting uncertainty and testing the model by predicting independent validation data.
Checkpoint and reflection¶
Discuss the questions below with a supervisor. Think if you have any additional questions regarding the lab or systems biology and feel free to discuss this with a supervisor
Some summarizing questions to discuss
- Look back at the lab, can you give a quick recap of what you did?
- Why did we square the residuals? And why did we normalize with the SEM?
- Why is it important that we find the "best" parameter sets when testing the hypothesis? Do we always have to find the best?
- Can we expect to always find the best solution for our type of problems?
- What are the problems with underestimating the model uncertainty? And with overestimating?
- If the uncertainty is very big, how could you go about to reduce it?
- Why do we want to find core predictions when comparing two (or more) models? What are the possible outcomes if we did the experiment?