Introduction to modelling for 13C metabolic flux analysis (MFA)¶

Author: Nicolas Sundqvist.

The text and figures explaining the theoretical concepts explored in this computer exercise is taken from the PhD-thesis of Nicolas Sundqvist with the author's consent.

You can download these files here. Download and extract the files to a suitable locations or clone them from the git repository. Data files for the exercise can be found here Peak Areas and Net Uptake Release Data or at the respective links embedded in the text below.

Power-point slides are available here: With Animations, Without Animations, or as PDF

This exercise will assume that you are somewhat familiar with the concepts of:

ODE- model formulation
Quantitative model evaluation.
Statistical hypothesis testing.
Parameter estimation.
Model uncertainty analysis.

Theoretical background¶

A more detailed theoretical introduction to ¹³C MFA is planned to be presented here. However, until such text is fully implemented a good place to start is Nicolas Sundqvist's Ph.D. thesis, which can be found here. Specifically, sections 2.2 and 4.3 of this thesis introduces the field of MFA.

Below is an example of how the Elementary Metabolite Unit (EMU) decomposition algorithm, presented by Antoniewicz et al., 2007, is implemented for a small model.

Detailed EMU decomposition

This image illustrates a small metabolic model with three reactions and file metabolites. In this example capital letters are used to indicate metabolites while lower-case letters are used to indicate the position of specific carbon atoms within a reaction.

The metabolites are:

$A$. With two carbon atoms.
$B$. With one carbon atom.
$C$. With three carbon atoms.
$D$. With two carbon atoms.
$E$. With one carbon atom.

The reactions are:

Reaction $\nu_1$ combines metabolites $A$ and $B$ to form metabolite $C$. The two atoms in $A$ become the two first atoms in $C$, and the atom in $B$ becomes the third atom in $C$ (A + B = C | ab + c = abc).
Reaction $\nu_2$ cleaves metabolite $C$ into metabolites $D$ and $E$. The first atom in $C$ becomes the lone atom in $E$, and the two last atoms in $C$ becomes the atoms in $D$ (C = D + E | abc = bc + a).
Reaction $\nu_3$ transforms metabolite $E$ to metabolite $B$. Both metabolites $E$ and $B$ have only one carbon atom the carbon structure does not change. (E = D | a = a)

Let us assume that metabolites $A$ and $B$ are known inputs/substrates and we want to simulate the labelling distribution for metabolite $D$. This means that we want to calculate the EMU that corresponds to the full $D$ molecule, i.e. $D_{12}$. The bolom left of the image above illustrates the complete EMU decomposition from $D_{12}$. This decomposition identifies all EMUs required to calculate $D_{12}$ from the known substrates. Note that the list of required EMUs are shorter that the list of all possible EMUs. For instance, EMUs such as $C_{123}$ and $A_{12}$ are not required for this example.

We can take the different reactions in the EMU decomposition list and reconstruct two small networks of EMUs. One network for all EMUs of size two and one network for all EMUs of size 1. We can then formulate the equation for each EMU "State" as an ODE based on the EMU networks. Since we assume that we are at steady-state the derivative of each state will be equal to 0. Here we also write out the states within the same EMU network with the coefficient 0, such that each equation (within an EMU network) depends on all other states of the same size. The reason for this will become apparent when we convert the equations to a matrix structure at a later stage.

$\dot{A_1} = - \nu_1*A_1 + 0*C_1 + 0*E1 + 0*B_1 = 0$

$\dot{C_1} = \nu_1*A_1 - \nu_2*C_1 + 0*E_1 + 0*B_1 = 0$

$\dot{E_1} = 0*A_1 + \nu_2*C_1 - \nu_3*E_1 + 0*B_1 = 0$

$\dot{B_1} = 0*A_1 + 0*C_1 + \nu_3*E_1 + \nu_1*B_1 = 0$

$\dot{C_{23}} = \nu_1 *(A_2 \times B_1) - \nu_2*C_{23} + 0*D_{12} = 0$

$\dot{D_{12}} = 0*(A_2 \times B_1) + \nu_2*C_{23} + 0*D_{12} = 0$

The equations now can be reformulated by moving all "known" input EMUs to the right hand side. Here we also divide the equations by EMU size. Please note that for EMU size 2 $B_1$ is considered a "known" EMU since $B_1$ can be solved by solving the third equation of EMU size 1. Such that:

EMU size 1, network 1

$\begin{matrix} 0*C_1 & + & 0*E1 & + & 0*B_1 & = & \nu_1*A_1\\ -\nu_2*C_1 & + & 0*E_1 & + & 0*B_1 & = & -\nu_1*A_1\\ \nu_2*C_1 & - &\nu_3*E_1 & + & 0*B_1 & = & 0*A_1\\ 0*C_1 & + & \nu_3*E_1 & + & \nu_1*B_1 & = & 0*A_1 \end{matrix}$

EMU Size 2, network 1

$\begin{matrix} -\nu_2*C_{23} & + & 0*D_{12} & = & -\nu_1 *(A_2 \times B_1) \\ \nu_2*C_{23} & + & 0*D_{12} & = & 0*(A_2 \times B_1) \end{matrix}$

We can now see that if the input EMU $A_1$ is known we can sequentially solve for all other EMUs for a given flux configuration $v$. To condense these calculations further we can reformulate each EMU network as a single matrix equation. Please note that we can ignore the first equation for EMU size 1, since all coefficients on the left hand side are 0 this equation will not add any information to the system (This is the effect of A being the system substrate). Such that:

$\begin{bmatrix} -\nu_2 & 0 & 0 \\ \nu_2 & -\nu_3 & 0 \\ 0 & \nu_3 & \nu_1 \\ \end{bmatrix}$ $\begin{bmatrix} C_1\\ E_1\\ B_1\\ \end{bmatrix}=$ $\begin{bmatrix} \nu_1 \\ 0 \\ 0 \\ \end{bmatrix}$ $\begin{bmatrix} A_1\\ \end{bmatrix}$

$\begin{bmatrix} -\nu_2 & 0 \\\nu_2 & 0 \\ \end{bmatrix}$ $\begin{bmatrix} C_{23}\\ D_{12}\\ \end{bmatrix}=$ $\begin{bmatrix} -\nu_1 \\ 0 \\ \end{bmatrix}$ $\begin{bmatrix} (A_2 \times B_1)\\ \end{bmatrix}$

Literature list

Here are a few starting references for the field of ¹³C MFA. As also stated above sections 2.2 and 4.3 of Nicolas' Ph.D. Thesis, and the references therein, is also a good starting point.

Antoniewicz, M. R. (2018) ‘A guide to 13C metabolic flux analysis for the cancer biologist’, Experimental & Molecular Medicine, 50(4), p. 19. doi: 10.1038/s12276-018-0060-y.
Dai, Z. and Locasale, J. W. (2016) ‘Understanding metabolism with flux analysis: From theory to application’, Metabolic Engineering, 43, pp. 94–102. doi: 10.1016/j.ymben.2016.09.005.
Buescher, J. M. et al. (2015) ‘A roadmap for interpreting 13 C metabolite labeling patterns from cells’, Current Opinion in Biotechnology, 34, pp. 189–201. doi: 10.1016/j.copbio.2015.02.003.
Sundqvist, N. et al. (2022) ‘Validation-based model selection for 13C metabolic flux analysis with uncertain measurement errors’, PLOS Computational Biology, 18(4), pp. 1–27. doi: 10.1371/journal.pcbi.1009999.
Antoniewicz, M. R., Kelleher, J. K. and Stephanopoulos, G. (2007) ‘Elementary metabolite units(EMU): a novel framework for modeling isotopic distributions.’, Metabolic engineering, 9(1), pp. 68–86. doi: 10.1016/j.ymben.2006.09.001.
Antoniewicz, M. R., Kelleher, J. K. and Stephanopoulos, G. (2006) ‘Determination of confidence intervals of metabolic fluxes estimated from stable isotope measurements.’, Metabolic engineering, 8(4), pp. 324–37. doi: 10.1016/j.ymben.2006.01.004.
Shupletsov, M. S. et al. (2014) ‘OpenFLUX2: 13C-MFA modeling software package adjusted for the comprehensive analysis of single and parallel labeling experiments’, Microbial Cell Factories, 13(1), p. 152. doi: 10.1186/s12934-014-0152-x.

Practical computer exercise¶

For this exercise we will study a fictional micro physiological system consisting of liver tissue, and muscle tissue connected by a circulatory system. Your task is to study the central glucose metabolism of this system and to create estimates for the intracellular metabolic fluxes. Furthermore, you will investigate how the metabolic fluxes change between a healthy system and a system modified to represent diabetic progression. Please note that this is a fictional system and that all data presented in this exercise is generated in silico.

Metabolic Model (Click to expand)

The model we will use for this exercise is inspired by the example presented in Antoiewicz et al. 2006. The model has been slightly modified to suit this pedagogical exercise. This model represents the main metabolic pathways of the glucose metabolism in the muscles and the liver. Included in the model are simplified interpretations of the glycolysis and the pentose phosphate pathway (PPP) in the muscles, and the tricarboxylic acid (TCA) cycle, gluconeogenesis, ketogenesis, and lipolysis in the liver. Between these pathways the model includes a total of 30 metabolic fluxes described in detail in Table 1 and depicted in Figure 1.

The model has two main inputs glucose and lactate. Additionally, there are fluxes that represent the endogenous storage and breakdown of glycogen, glycerol, and fatty acids (FA). The system's outputs are Glucose, Lactate, Ketone bodies, and CO₂.

Table 1: Detailed model breakdown.

Flux	Reaction	Atom mapping	Compartment
$v_1$	Glucose Source -> Glucose	abcdef -> abcdef	Source -> Blood
$v_2$	Glucose -> G6P	abcdef -> abcdef	Blood -> Muscle
$v_3$	G6P -> 2x G3P	abcdef -> cba + def	Muscle
$v_4$	G6P -> R5P CO2	abcdef -> bcdef + a	Muscle
$v_5$	2x R5P -> S7P + G3P	abcde + ABCDE -> abABCDE + cde	Muscle
$v_6$	S7P + G3P -> G6P+ E4P	abcdefg + ABC -> abcABC + defg	Muscle
$v_7$	R5P + E4P -> G6P + G3P	abcde + ABCD -> abABCD + cde	Muscle
$v_8$	G3P -> Pyr	abc -> abc	Muscle
$v_9$	Pyr -> Lac	abc -> abc	Muscle -> Blood
$v_{10}$	Lac Source -> Lac	abc -> abc	Source -> Blood
$v_{11}$	Lac -> Lac Output	abc -> abc	Blood -> Output
$v_{12}$	Lac -> Pyr	abc -> abc	Blood -> Liver
$v_{13}$	Pyr + HCO3 source -> OAC	abc + A -> abcA	Liver
$v_{14}$	Pyr + CoA -> AcCoA + CO2	abc + X -> ab + c	Liver
$v_{15}$	OAC + AcCoA -> SucCoA + 2x CO2	abcd + AB -> ABbc + a + d	Liver
$v_{16}$	SucCoA -> Fum	abcd -> abcd	Liver
$v_{17}$	Fum -> OAC	abcd -> abcd	Liver
$v_{18}$	OAC -> Fum	abcd -> abcd	Liver
$v_{19}$	FA Source -> AcCoA	ab -> ab	Liver
$v_{20}$	2x AcCoA -> Ketone	ab + AB -> abAB	Liver
$v_{21}$	OAC -> PEP + CO2	abcd -> abc + d	Liver
$v_{22}$	PEP -> G3P	abc -> abc	Liver
$v_{23}$	PEP -> Pyr	abc -> abc	Liver
$v_{24}$	Glycerol Source -> G3P	abc -> abc	Liver
$v_{25}$	2x G3P -> G6P	abc + ABC -> cbaABC	Liver
$v_{26}$	Glycogen Source -> G6P	abcdef -> abcdef	Liver
$v_{27}$	G6P -> Glucose	abcdef -> abcdef	Liver -> Blood
$v_{28}$	Glucose -> Glucose Output	abcdef -> abcdef	Blood -> Output
$v_{29}$	CO2 -> CO2 Output	a -> a	Muscle-> Output
$v_{30}$	CO2 -> CO2 Output	a -> a	Liver -> Output

Experimental data

The data used for this exercise consists of two distinct types of data sets. The first data set is a compilation of the peak areas from the mass spectrometry (MS) chromatogram.

These values can be found in the file PeakAreas.xlsx (file). This peak area data consists of a table where the rows contain the data for the different metabolites and the columns represent the individual repeats for the three different experiments. More specifically, each row represents a unique mass-to-charge ratio in the spectrogram, or in other words a specific mass isotopomer (MI) for a specific metabolite. Likewise, each column represents a single experimental repeat of one of three different experiments:

Healthy Glucose - representing healthy conditions with a fully saturated glucose tracer (U-13C Glucose) i.e. glucose with fully saturated ¹³C in all six carbon atoms. All other inputs are completely unlabelled (¹²C).
Healthy Lactate - representing healthy conditions with a fully saturated Lactate tracer (U-13C Lactate) i.e. Lactate with fully saturated ¹³C in all three carbon atoms. All other inputs are completely unlabelled (¹²C).
Diabetic Glucose - representing diabetic conditions with a fully saturated glucose tracer (U-13C Glucose). All other inputs are completely unlabelled (¹²C).

For each experiment the labelling distributions for following metabolites have been measured:

Glucose
Glucose 6-phosphate (G6P)
Glyceraldehyde 3-phosphate (G3P)
Pyruvate (Pyr)
Lactate (Lact)
Succinyl-CoA (SucCoa)
Fumarate (Fum)
Carbon dioxide (CO2)

The MIDs for these metabolites, for each experiment can be depicted as:

Task 1: Formulate the model.

Let's start by formulating the model described in the box above.

Formulate the model for the reactions depicted in Figure 1.
- Use the atom mappings detailed in Table 1.
Formulate the appropriate list of "excludedMetabolites"
Formulate the appropriate list of "simulatedMDVs"

For this example, we have measurements for Glucose, G6P, G3P, Pyruvate, Lactate, Succinyl-CoA, Fumarate, CO2.
Formulate the appropriate list of "inputSubstrates"

Save the model file and save a copy as a tab-delimited .txt file. This text file is the file openFlux will use.

OpenFLUX2 Model formulation

OpenFLUX2 requires the model structure to be formulated as a tab-delimited .txt file. However, the easiest way to edit the model structure is in an excel spreadsheet and save it as a tab-delimited .txt file. The complete manual for the OpenFLUX2 toolbox can be found here, and in the "OpenFLUX_v2.1_Windows" folder of the toolbox. This manual contains a detailed description for how to formulate the metabolic models for OpenFLUX2. Here will follow an abbreviated description.

The model file-structure
OpenFLUX2 relies on the fact the each unique model structure has its own folder. This folder is in this exercise referred to as the Model project folder. OpenFLUX2 will on several occasions read and write to/from this folder. Your model name should therefore be the name of this folder. Personally, I like to structure my model folders in a Specific "Models"- folder, such that I can keep the different model folders clean from Data-, result-, and script files.

Model Definition

Model Table structure

OpenFLUX2 defines the model structure in a table with the row representing different fluxes and the columns represents Flux ID (RxnID), reaction stoichiometry (rxnEq), Atom mappings (rxnCTran), any known flux rates (rates), the reaction type (rxnType), An indication if the flux is part of the basis fluxes subset (basis).

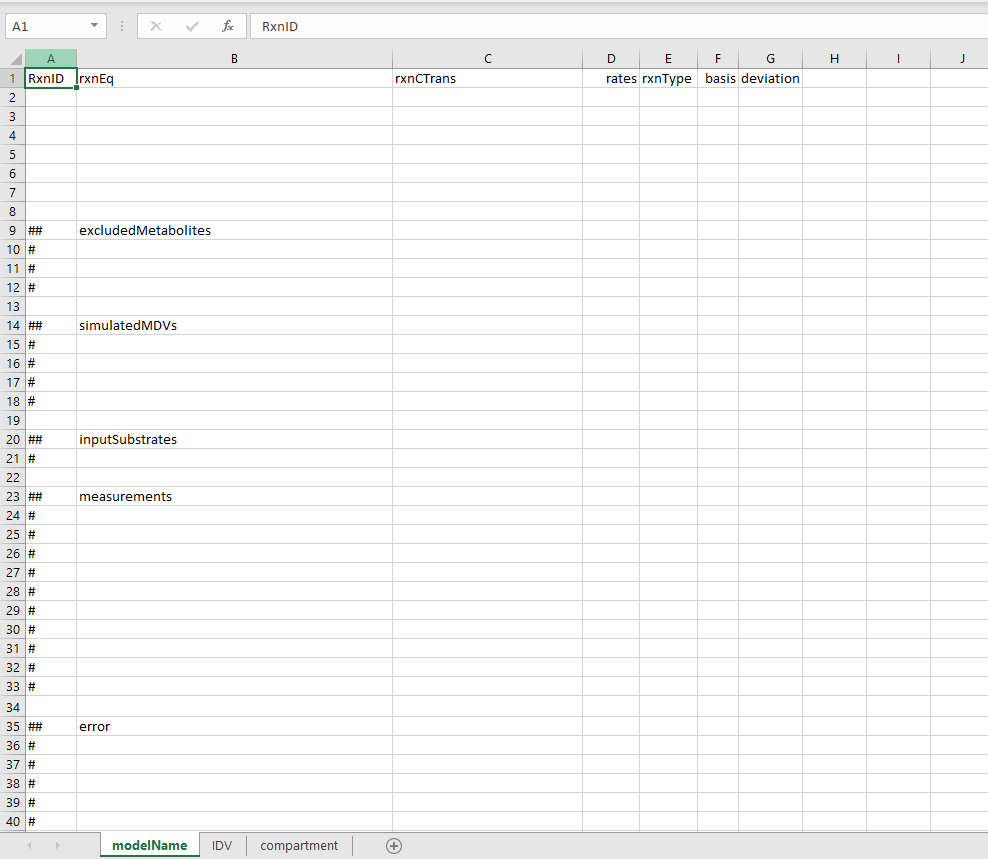
Flux ID: This entry should be a string that uniquely identifies the flux. It could be e.g. "V1", "PDH", or "GLC_IN".
Reaction stoichiometry: This entry specifies the stoichiometry of the reactions substrates and products.
- Names of metabolic species are case sensitive and have to be consistent across different reactions. The reaction should be structure as:
```
substrate1 + substrate2 = product1 + product2 
```
With spaces surrounding the '+'- and '='-signs. - Note that the stoichiometric coefficients of all reactants must be 1. This means that reactions involving multiple reactants of the same metabolite must be defined as separate reactants e.g.
```
Glucose = Pyr + Pyr 
```
- All fluxes are defined as positive. Meaning reversible fluxes are defined in two separate parts. One forward reaction and one Reveres reaction.
Atom mapping: Follows the same structure as the reaction stoichiometry column. Important to think of when defining the atom mappings are:
- Atom maps are defined by case sensitive alphabetic characters [a-z] and [A-Z]. With the exception for the characters "x" and "X".
- Positional mapping is used to assign each atom transition formula in the carbon transition equation to its respective metabolite in the reaction equation. I.e. the first atom map should correspond to the first reactant in the prior column. e.g.
```
Glucose = Pyr + Pyr | abcdef = abc + def
```
- Atom mapping is uniquely conserved within each reaction. Meaning the character "a" specifies how atom "a" transition from substrate to product within that specific reaction. Hence the same character "a" can be used for multiple reactions but the position is unique for every reaction.
- The characters "x" and "X" are reserved to indicate reactants that do not contain any traceable atoms e.g. no carbon atoms if a carbon tracer is used. Such metabolites are excluded from the EMU balancing. For example:
```
Pyr + CoA = AcCoA + CO2 |abc + X = ab + c 
```
Reaction rates are optional and should in most cases be left empty at this stage.
Reaction type: There are a few different reaction types that can be specified in OpenFLUX2. These tags are case sensitive.
- F - Indicates a simple forward reaction. If you are unsure of the reaction type it is probably a forward reaction.
- R - Indicates the reaction as the reverse direction in a reversible reaction.
- FR - Indicates the reaction as the forward direction in a reversible reaction.
- B - Indicate that the reaction should be excluded from the isotopomer balance. All of the system's outflow fluxes should be reaction type "B".
- BR - Indicate that the reaction should be excluded from the isotopomer balance (same as type "B"), but are also allowed to have a negative value.
- There are also S and SF type reactions that indicate if a reaction should be excluded from the stoichiometric metabolite balance. These reaction types are for more niche cases and detailed descriptions can be found in the OpenFLUX2 manual.
Basis: This is a flag that indicates whether a reaction should be considered a free independent flux. Such fluxes are flagged with a "x".
The last column specifies a deviation for a specified invariant basis value. This should be empty if basis fluxes are only indicated by "x". Please see OpenFLUX2 manual for further details.

Model List structure

In addition to the model reaction definition table above, the model file should also contain five lists specifying metabolites with special properties such as network inputs and outputs. These file lists are specified below the reaction table and are indicated by a double hashtag "##" for list headline and a single hashtag "#" for list entries (see figure above). These lists are:

excluded Metabolites - This list contains the names of metabolites, defined in reaction table, to be excluded from the metabolite balance model. These are typically the input and output metabolites. The list could also contain metabolic co-factors such as ATP or NADH, if these should be excluded from the stoichiometric balance constraint.
```
## excludedMetabolites
# Glucose_IN 
# Lactate_IN
# CO2_OUT
#FA_OUT
```
simulatedMDVs - This list contains the names of the metabolites that are to be simulated, typically these are the metabolites that have been measured. in addition to the metabolite name the entry should also specify what fragment of the metabolite should be simulated. This is indicated by a hashtag "#" followed by a binary sequence that specifies the fragment. For example, if we want to simulate the full MID for pyruvate that has thee carbon atoms the list entry would be:
```
## simulatedMDVs
# Pyr#111
```
If we instead for some reason wanted to simulate the MID that correspond to only the first two carbon atoms of pyruvate the entry would look like
```
# Pyr#110
```
Note that the total number of 1 and 0 should always correspond to the total number of tracked atoms in the corresponding metabolite.
inputSubstrates - This list specifies the names of the network substrates that will affect the labelling distributions, i.e. the metabolites that represent the labelled tracers.
measurements - This list is not used in this modified version of OpenFLUX2. The list would be used to specify the measured MID values for the metabolites specified in the simulatedMDVs list. For this modified version of OpenFLUX2 this list can be left empty as we will specify the measurement values at a different stage.
error - This list is not used in this modified version of OpenFLUX2. Similarly to the measurement list above, this list contains the corresponding measurement error values for each measured metabolite, and for the same reason this list can be left empty.

The Model table - and Model List structure boxes above should explain the basics required for a complete model definition. But there are some additional aspects that are useful to be aware of for defining various types of flux models. These aspects are explored in the boxes below.

Model compartments

If we have a model with fluxes in and between different compartments, metabolites in these different compartments are treated as unique metabolites. For instance, if we have pyruvate in both the cytosol and the mitochondrial matrix, we could indicate this by e.g. adding a suffix to the metabolite name such as

Pyr_C = Pyr_M
...

## simulatedMDVs
# Pyr_C#111
# Pyr_M#111

Note that in this example the model considers Pyr_C and Pyr_M to be different metabolites thus both must be listed in the simulatedMDVs list if we want to simulate the total amount of pyruvate in our system. Note also that the suffix _e is specifically reserved to represent external metabolites i.e. metabolites that should not contribute to the measurement equation.

Symmetric molecules

Some metabolites have completely symmetric molecules, meaning it is impossible to uniquely label the individual atoms. One such example is Fumarate/Fumaric acid which has four carbon atoms, but due to the symmetric structure you can't tell the "first" carbon atom from the "fourth" carbon atom, see figure below.

Such symmetric molecules present a problem since we rely on being able map the individual atom transitions and thus label each carbon atom "a", "b", ... etc. To resolve this problem we can define any reaction that produces a symmetric molecule as producing two versions of that molecule. We also introduce coefficients that specify how much of each version the reaction produces.

OAC = 0.5 Fum + 0.5 Fum  |  abcd = 0.5 abcd + 0.5 dcba

In this example we specify that the reaction that turns oxaloacetic acid (OAC) to Fumarate produces 50 % Fumarate with the carbon configuration "abcd" and 50 % with the configuration "dcba".

Inflow/Outflow Fluxes

Since the model has to balance the fluxes such that everything that the net flux through the network is equal to 0 the input and output fluxes need to be handled a bit differently from the rest. The easiest way to deal with the network boundaries is to model the inputs and outputs as their own compartments. Thus, only the metabolites in these input/output compartments need to be listed as excluded Metabolites. An example of this can be seen below where the model uptake of glucose and output of glucose are defined as specific fluxes.

v_glc_IN    Glucose_IN = Glucose_Blood
v_glc_OUT   Glucose_Blood = Glucose_OUT

Once we have a fully defined model structure, we will use OpenFLUX2 to parse this model text file into the EMU model structure. This is the part where we run the EMU decomposition algorithm.

Task 2: Compile the model

Follow the following steps to compile the EMU model from the model definition.

Navigate to the "OpenFLUX_v2.1_Windows" folder in the toolbox repository.
Run the "OpenFLUX_v2.jar" script - Make sure you have Java installed. From the directory "./OpenFLUX_v2.1_Windows" run the following command.
```
    java -jar OpenFLUX_v2.jar 
```

This should open the following window.

Set the "Project Folder" field to the directory of the Model folder.
Set the "Model file" field to the name of the model .txt file.
For the initial model compilation, Tick the "Overwrite all existing files" option.
Press the "Generate Model" button.

OpenFLUX will tell you if it encounters anything it thinks is out of place. Once successful 21 new files should have been created, 16 in the "model"-folder and 5 in the project folder. See figure.

Potential compilation errors

There are a few compilation errors where OpenFLUX2 will crash rather that specifying and error message. Here is a list of a few of these errors and what might be the issue.

An error starting with the line "Exception in thread "AWT-EventQueue-0" java.lang.StringIndexOutOfBoundsException: begin 0, end -1, length 17" likely referees to an incompatible equation in a reaction definition. Something like a reaction missing an equal sign or similar.
An error starting with the line "Exception in thread "AWT-EventQueue-0" java.lang.ArrayIndexOutOfBoundsException: Index 1 out of bounds for length 1" likely referees to an misdefined entry in one of the lists (excludedMetabolites, simulatedMDVs, or inputSubstrates). Something like a typo or a missed "#111" entry for the simulatedMDVs.

If you encounter an error not specified in the list above the best approach is to very thoroughly go through each aspect of the model definition and try to identify any issues. If reasonable you could also try to systematically reduce the model complexity until you have found what might cause the error. Reducing model complexity may include but is not limited to:

Removing reversible reactions.
Removing metabolic Co-factors
Reducing the number of excluded metabolites.

If you encounter and solve an error that is not specified in the list above. Please feel free to expand the list to include this error.

Now that you hopefully have a full EMU model, we will look at how we want to formulate the other components required to simulate the model and compare the simulation to the experimental data. Starting with looking at how we define the model input substrates.

Substrate definition - Model Inputs

To define the model substrate, we need to fully define the MIDs for all required substrate EMUs. The substrate EMUs are determined by the EMU decomposition algorithm. The substrate MIDs can be calculated if one knows the isotope enrichment configuration of each substrate.

This isotope enrichment vector specifies the fractional purity of the isotope of each atom in the substrate. For instance, glucose that are 100 % enriched with ¹³C ([U-13C] Glucose) would have an enrichment vector of [1 1 1 1 1 1]. Glucose that are 100 % enriched with ¹³ C in carbon atoms 1 and 3 ([1,3 -13C] Glucose) would an enrichment vector of [1 0 1 0 0 0].

Natural Isotope abundance

Depending on which stable isotope is used for the labelling there will be a natural abundance of this isotope in circulation. This natural abundance needs to be taken into account since it will affect the MIDs. There are methods of adjusting the calculated MIDs for this natural abundance before the comparison with experimental data. But it is also possible to define any unlabelled inputs to have an enrichment corresponding to this natural abundance. For ¹³C the natural abundance is around 1.07%. This means that glucose that are completely unlabelled ([U-12C] Glucose) would have an enrichment vector of [0.0107 0.0107 0.0107 0.0107 0.0107 0.0107].

Additionally, for practical reasons it is nearly impossible to achieve a 100 % isotope enrichment in any media. This means that 99 % is a better approximation for fully enriched substrates. Thus, if nothing else is specified, for ¹³C it is recommended to use an enrichment value of 0.99 for fully labelled substrates and 0.0107 for unlabelled substrates.

The OpenFlux2 toolbox used in this exercise uses the script subsDef to manually define the substrate enrichment vectors.

Please note that subsDef must be used in the Model project folder. Since it relies on the specific structure of the model.

How to use subsDef

The script subsDef allows the user to manually define the labelling configuration of the input substrates. This script determines what is a system input based on the file ./model/inputSubstratesEMU.txt, which in turn is created by the OpenFLUX2 parser during the model definition step. Please note that all system inputs will need to be defined, not just labelled inputs. Upon running the script subsDef the user will be prompted to enter the vector describing the isotope enrichment configuration of each substrate.

AAV - Atom abundance value.

specify the 13C atom activity vector of input substrates
example, 1,2-13C Glucose at 99% enrichment purity is
>>0.99 0.99 0.0107 0.0107 0.0107 0.0107
specify AAV of FA_IN(should consist of 2 elements) >>

You will also be prompted to specify if there are multiple input pools for each substrate, i.e. do you e.g. have a mixture of both labelled and unlabelled substrate in the input media, and what the ratio between these input pools are. The sum of all these ratios should sum to 1 for all pools of each substrate.

specify AAV of FA_IN(should consist of 2 elements) >>1 1
specify another AAV for FA_IN (1-YES, 0-NO) [0]>>1
specify AAV of FA_IN(should consist of 2 elements) >>0 0
specify another AAV for FA_IN (1-YES, 0-NO) [0]>>
mixture of 2 FA_IN substrates were used, specify ratios >> 0.5 0.5

In the example above we have a mixture of two pools of Fatty Acids (FA), the first pool is 100 % enriched with ¹³$C and the second pool is completely unlabelled. The ratio between these two pools is 1/1 i.e. 50/50.

After all substrates have been defined there will be a cell-array variable available in the workspace called substrateInfo. This variable contains all the information entered by the user. The structure of this variable is determined by the OpenFLUX2 toolbox and will be used at a later stage to configure all substrate MIDs. You can save the substrateInfo-variable to avoid having to manually enter the same substrate information multiple times.

The script subsDef will result in a cell-array variable called substrateInfo. That contains all the vital information regarding the substrate enrichment.

The substrateInfo cell-array

The cell-array substrateInfo is structured to allow OpenFLUX2 to calculate the MIDs for all required substrate EMUs. The variable has the following structure

substrateInfo = 

{'FA_IN'      }    {[2]}    {1×2 cell}    {[0.5 0.5]}
{'Gluc_IN'    }    {[6]}    {1×1 cell}    {[1]}
{'Lact_IN'    }    {[3]}    {1×1 cell}    {[1]}

Where the first column contains the name of the substrate as defined in the model definition under the inputSubstrates-list. The second column contains a vector with the number of labelled atoms in the substrate. The third column contains the isotope enrichment vectors for each substrate, and the fourth column contains the ratio of input pools for each substrate. In the case that there are multiple input pools for a specific substrate, the entries in the third and fourth column will have multiple elements.

It is also possible to read the substrate enrichment information from a text file with the function readSubstrateInfoFromFile(fileName). The readSubstrateInfoFromFile(fileName)-function will result in the same substrateInfo cell-array as subsDef

How to use readSubstrateInfoFromFile - function

The function readSubstrateInfoFromFile(fileName) takes a single input in the form of a string containing the file name of the text file with the substrate enrichment information specified. This file should be a tab-delimited .txt-file that is saved in the Model project folder. The text file should have the following structure:

Metabolite ID   Mixture fraction    Atom probabilities
FA_IN           0.5                 0.0107  0.0107
FA_IN           0.5                 0.99    0.99
Gluc_IN         1.0                 0.99    0.99    0.99    0.99    0.99    0.99
Lact_IN         1.0                 0.0107  0.0107  0.0107

It is important that the Metabolite ID for each substrate is the same as specified in the model definition under the inputSubstrates-list. The Mixture fraction specifies the ratio of the substrate pool with the enrichment specified by Atom probabilities.

The function returns the same cell-array substrateInfo as obtained from the script subsDef. The function also saves the imported substrate information on the Model project folder in a file called inputSubConfig.mat.

Conversely, if you have the substrateInfo cell-array it is possible to export it to a text file by using the exportSubstrateInfoToFile-function.

How to use exportSubstrateInfoToFile -function

The function exportSubstrateInfoToFile writes the information contained in the substrateInfo cell-array to a tab-delimited txt-file. The function takes two inputs. The first input is the substrateInfo cell-array defined by the subsDef-script. The second argument is a sting specifying the name of the text file in which the substrate information is saved. The second input, the file name, is optional. If no file name is provided a generic temporary file name is chosen.

If we have the following substrateInfo cell-array:

substrateInfo = 

{'FA_IN'      }    {[2]}    {1×2 cell}    {[0.5 0.5]}
{'Gluc_IN'    }    {[6]}    {1×1 cell}    {[1]}
{'Lact_IN'    }    {[3]}    {1×1 cell}    {[1]}


exportSubstrateInfoToFile(substrateInfo, 'GlucoseSubstateInfo')

The exportSubstrateInfoToFile -function results in the following text file

Metabolite ID   Mixture fraction    Atom probabilities
FA_IN           0.5                 0.0107  0.0107
FA_IN           0.5                 0.99    0.99
Gluc_IN         1.0                 0.99    0.99    0.99    0.99    0.99    0.99
Lact_IN         1.0                 0.0107  0.0107  0.0107

The data obtained from isotope labelling experiments usually require some degree of post-processing before we have MIDs that we can compare with our model simulation.

How to calculate the MIDs from the raw peak-data

When measuring the labelling distributions, the raw data will be in the form of a spectrogram, regardless if you measure via mass spectrometry (MS) or magnetic resonance spectroscopy (MRS). This spectrogram will consist of a series of peaks for molecules with different mass-to-charge ratios (m/z). Thus, we can obtain a peak for each mass isotopomer. The area under the curve (AOC) for each peak will be proportional to the abundance of that specific mass isotopmer. Since the MID for a given metabolite is the relative abundance of each mass isotopmer we can calculate the MID from the peak areas. Simply calculate the sum of all peak areas for the same metabolite and divide each element with this sum to get the relative abundance of each mass isotopmer for that metabolite.

$MID_{X} = \frac{PeakArea_{X_{i}}}{\sum_{\forall i}^{} PeakArea_{X_{i}}}$

Here $X$ indicates a metabolite and the index $i$ indicates mass isotopomers of metabolite $X$.

Here is a very simple example of what this calculation could look like.

Metabolite	MI	Peak Area	MID
Pyruvate	0	300	0.30
Pyruvate	1	250	0.25
Pyruvate	2	50	0.05
Pyruvate	3	400	0.40
Total		1000	1

Both of the boxes above are related to the labelling experiment(s) that we have performed i.e. the experimental conditions of the labelled substrates and the resulting Peak area/MID data. Thus, it is reasonable to structure this information together such that when we simulate the model we have all related information in the same structure. This will also avoid potential confusion should we wish to simulate multiple experimental conditions simultaneously e.g. multiple parallel labelling experiments.

Task 3: Structure the MID data and model inputs

The file PeakAreas.xlsx contains the raw peak area data for the three experiments described in the "Experimental data"-box above.

Your task is to write a function/script that:

Reads the data from the spreadsheet file.
Calculate the MIDs for the respective metabolites.
Calculate the mean MIDs for each metabolite, and the corresponding standard error of the mean (SEM), for each respective experiment.
Define the model substrate enrichments for each experiment, using either the subsDef script or the readSubstrateInfoFromFile-function (see description above).
Structure the MIDs mean and SEM data along with the substrate enrichment information for each respective experiment in a suitable way.
- See the description of the Experiment object class below for a suggested way to structure the information.
Save the structured information in a suitable way.
- If you are using the Experiment-class to structure the experiment information. You can save all Experiment-objects in a .mat-file in the Model project folder, This file should have the name Expts.mat. This will ensure compatibility with additional functions in the toolbox.

There are of course various different ways of structuring the information of measurement data, and substrate input. One suggested approach built into the modified OpenFLUX2 toolbox is the Experiment object class. This Matlab class simply structures the information in a pre-defined way such that it is easy to save and work with.

The Experiment object class

The Experiment class is a Matlab-object class defined in the modified OpenFlux2-toolbox used in this exercise. The class has the following properties.

description - a text description of the Experiment set up.
id - a 1-by-m cell matrix with the id of each metabolite, m is the number of metabolites relevant for the experiment.
msData - a n-by-m cell matrix with the MID-data for the experiment n is the number of datasets and m is the number of metabolites/states.
error - a same sized n-by-m cell matrix as msData that contains the corresponding measurement error.
tracer - a text string with the name of the tracer used in the experiment.
substrateInfo - a k-by-4 cell matrix containing the labeling composition of the system substrates, k is the number of system substrates. This matrix is defined by the subsDef.m script.
result - a result structure of class results.m that contains the result of a parameter estimation for the experiment.

Define a new Experiment object using the SetUpExpt-function

The SetUpExpt-function allow you to define an Experiment object. The function takes three input arguments:

Measurements - a column vector containing all measurement points. I.e. all MIDs concatenated to a single vector. The order of the MIDs should correspond to the inputSubstrates-list in the model definition.
Error - a column vector containing the measurement error of each measurement point. Structured in the same way as the Measurements input.
substrateInfo - the substrateInfo- cell-array. See detailed description in the "Substrate definition - Model Inputs" section above.

Suppose you have your MIDs and measurement error in a concatenated vectors as:

    measurements =[
    0.2221
    0.0538
    0.0069
    ...
    0.1726
    0.2996
    0.7004]

    error =[
    0.0230
    0.0157
    0.0067
    ...
    0.0680
    0.0520
    0.0520]

Please note that the ... notations indicates multiple additional rows. For the example data in the PeakAreas.xlsx file the corresponding measurements and error vectors should have 38 elements each.

Once you call the SetUpExpt-function you will be prompted to enter a name for the experiment object. Please not that this object will be a matlab variable and thus must have a viable matlab variable name.

    SetUpExpt(measurements, error, Diabetic_Glucose.substrateInfo)

    ----------Setting up new OpenFlux experiment----------
    Enter the experiment name (must be a viable MATLAB variable name) >>

Next you will be prompted to enter a description for the experiment. This should simply be a text string that describes this specific experiment.

    Enter experiment description >>

Lastly, you will be asked to enter the tracer configuration for this experiment. This is again a text string that specifies the tracer used in the experiment.

    Enter the tracers name >>

Once the function is done the output should be a new Experiment object.

    ans = 

    Experiment with properties:

          description: {'Labelled glucose for healthy condition'}
                   id: {'Gluc'  'G6P'  'G3P'  'Pyr'  'Lact'  'SucCoA'  'Fum'  'CO2'}
               msData: {8×1 cell}
                error: {8×1 cell}
               tracer: {'[U-13C]Glucose'}
        substrateInfo: {6×4 cell}
              results: [1×1 results]

The function will also save all experiment objects defined in a .mat file in the current directory. This file will be named Expts.mat. Please note that changing this file name might interfere with the functionality of other scripts and functions.

In order to calculate the MIDs for each metabolite, the function get_nIsotopomers might prove useful.

The get_nIsotopomers-function

This function returns a vector with the number of mass isotopmers for each metabolite specified in the "simulatedMDVs"-list, in the model definition. This function requires no input and generates one output, and should be called from the Model project folder. For example:

 nIsotopomers = get_nIsotopomers()
 nIsotopomers = 
    7
    7
    4
    4
    3

Remember that the number of mass isotopomers for a metabolite will be equal to the number of labelled atoms + 1 e.g. Glucose has 6 carbon atoms and will have 7 mass isotopomers $[M_{+0},M_{+1},M_{+2},M_{+3},M_{+4},M_{+5},M_{+6}]$.

Knowing the number of mass isotopomers for each metabolite is useful since it allows us to transform a vector with all MIDs to a structure with the MIDs for each metabolite isolated. For instance, the example below demonstrates how we can structure a matrix of MIDs (MIDsArray) as a cell-array.

MIDsCellStructure = mat2cell(MIDsArray,nIsotopomers,size(MIDsArray,2));

Each row of the MIDsCellStructure will be a cell containing the MIDs of the corresponding metabolite.

Calculate the input EMUS

Once you have the MID data and the substrate enrichment structured you can calculate the MIDs for all required substrate EMUs.

If you have the substrateInfo cell-array structure the function generateInputEMUs(substrateInfo) can be used to calculate and save all required substrate EMUs.

How to use generateInputEMUs(substrateInfo)- function

This function generates input EMUs based on the substrate isotope enrichment configuration and an optional input index specifying multiple simultaneous labelling configurations. It reads a pre-existing file inputSubstratesEMU.txt, defined by the model compilation and uses the genInSubEMU-function to process the substrate information and generate the input EMUs. The function saves the input EMUs as variables in a file named inputSubEMU1.mat. If multiple simultaneous labelling configurations are used call the function once for each labelling configuration and assign a unique integer value to index for each unique substrateInfo cell-array. This will create multiple inputSubEMU1.mat, inputSubEMU2.mat etc. files.

If you have the substrateInfo structure saved as part of an Experiment object you can use the Base_SetUp()-function to parse this information and calculate and save all required substrate EMUs.

How to use the Base_SetUp() function

This function incorporates some additional functionalities but also performs the same calculations and structuring achieved with generateInputEMUs(substrateInfo) (see description in the box above). This function takes two inputs Base_SetUp(Experiments, ExperimentNames), these are:

Experiments - a cell-array with an Experiment objects in each cell.
ExperimentNames - a cell-array with the corresponding names of each Experiment object in each cell.

The function should be called from within the Model project folder. If no input argument is provided the 'SelectExperiments()' function will be called to prompt the user to manually select one or more pre-saved experiments.

The function SelectExperiments()

The function SelectExperiments() allows the user to manually select one or more Experiment-objects pre-saved in the file Expts.mat. This function will generate two output arguments:

    [Experiments, ExperimentNames] = SelectExperiments();

Experiments - a cell-array with all selected Experiment objects structured into individual cells.
ExperimentNames - a cell-array with the corresponding names of each of the selected Experiment object.

This function naturally pairs well with the Base_SetUp() as the output from SelectExperiments() generates the input arguments to Base_SetUp().

    [Experiments, ExperimentNames] = SelectExperiments();
    Base_SetUp(Experiments, ExperimentNames)

SelectExperiments() can also be used to load specific Experiment objects from Expts.mat. If the name of the desired Experiment objects are provided as input arguments to SelectExperiments(), these Experiment objects will be loaded without the manual prompts. For example

    [Experiments, ExperimentNames]=SelectExperiments('Healthy_Glucose')

    Experiments =

    1×1 cell array

        {1×1 Experiment}


    ExperimentNames =

    1×1 cell array

        {'Healthy_Glucose'}

In addition to the MID data, we also have estimates for the systems uptake and release of substrates and products. These measurements provide a reference point for our otherwise relative flux estimates, since flux estimation based solely on MID measurements can only be quantified relative to each other.

Uptake/Release flux measurements

Measurements of uptake and release fluxes are foundational data for conducting ¹³C MFA. These measurements provide the boundary conditions for the metabolic network and are essential for normalization of the intracellular fluxes. This is important because it allows the comparison of fluxes between different experiments or physiological conditions. Furthermore, the measured uptake and release rates are used as constraints in the ¹³C MFA model. This means that the model is set up to only allow solutions where the calculated uptake and release rates match the measured ones. This helps in narrowing down the possible range of intracellular fluxes and makes the flux estimation problem more well-posed.

In practice, the uptake/release rates are implemented as additional data points that are considered during the evaluation parameter estimation.

Calculate uptake/release fluxes Please note that the measured uptake/release rates will often be the net release rate of a metabolite i.e. how has the abundance of metabolite $M$ in the media changed after the experiment compared to before the experiment. A positive value for the release rate means that the system has a net release of metabolite $M$. A negative value for the release rate and the system has a net uptake of metabolite $M$

There are multiple different ways of obtaining measurements for uptake and release rates depending on the experimental system and or the metabolites one wishes to measure. For this exercise these rates are provided in a spreadsheet with mean and SEM values for a few metabolites. On approach that should be mentioned is to estimate the uptake/release rates from peak area data. This approach will not be used for this exercise but is explained in the box below.

Calculate Uptake/Release rates from peak areas

You can also calculate the Uptake/Release rates from peak area values. To do this we need to have measurements from samples representing both the fresh media and the spent media i.e. measurements from just the media before and after the experiments. Please note that this is quite a crude estimation of the uptake/release rates but is better than nothing if nothing else is available.

let $A_i$ be the peak area for the spent media, for mass isotopomer i, and $A0_i$ be the peak area for the fresh media.

Get the relative change between the peak areas, $F =\frac{A_i}{A0_i}$.
Multiply this fraction with the metabolite medium concentration of the fresh media to get the concentration in the spent medium $C_{M,spent} = F*C_{M,fresh}$.
Take the difference in concentration between spent and fresh medium $\Delta C_M = C_{M,spent} - C_{M,fresh} \iff \Delta C_M = (F-1)*C_{M,fresh}$.
Multiply this difference with the sample volume to get the total change in mol over the incubation time $\Delta n_M = \Delta C_M * V_{sample}$.
Divide this change in mol with the incubation time to get the change in mol/h or rate of release of metabolite $M$ $Release rate_M = \frac{\Delta n_M}{t}$.

If this $Release rate_M$ is positive i.e. $C_{M,spent} > C_{M,fresh}$ the system has a net release of metabolite $M$. If $Release rate_M$ is negative the system have a net uptake of metabolite $M$

Task 4: Structure the Uptake/release data

The file NetUptakeReleaseData.xlsx (File)contain the uptake/release data for four metabolites Glucose, lactate, Glycogen, and Ketone bodies, for both the healthy and diabetic conditions. These fluxes are depicted in the figure below

Your task is to

Write a function that loads and structures this data in a suitable way.
- You are free to do this as you please, but you can see box below for a suggestion.

An important aspect to consider is that these measurements represent the net release of the respective metabolite. In other words, the quantity we want to compare with the data points difference between the simulated inflow and outflow of metabolite $M$. This leaves us with three possible cases, either out model contains both the influx and efflux, only the influx, or only the efflux of metabolite $M$. In the case that our model contain:

Both the influx and efflux of metabolite $M$ the net release of $M$ is equal to: $V_{M, OUT} - V_{M, IN}$.
Only the influx of metabolite $M$ the net release of $M$ is equal to: $- V_{M, IN}$.
Only the efflux of metabolite $M$ the net release of $M$ is equal to: $V_{M, OUT}$.

This means that to calculate the uptake/release fluxes from our simulated flux vector $V$ we need to know the index of these influxes/effluxes in the flux vector i.e. the index at which these influxes/effluxes are defined in the model file.

Structure the Uptake/release data in a table

Personally, I prefer to structure the uptake/release data as a Matlab table for each experimental condition. Please note that this is personal preference and far from the only way to structure this information. The important information to keep in mind is the flux indices that correspond to the influx/efflux of each metabolite. The table structure suggested here also specifies a coefficient which indicates if the flux is an influx or an efflux. Influxes get the coefficient -1 and effluxes get the coefficient 1.

For example, if we follow the model structure depicted in Figure 1, the influx of Glucose is defined as $\nu _1$ and the efflux of glucose is defined as $\nu _{28}$. Thus the fluxIdx for Glucose becomes [28 1] and the coefficients for Glucose become [1 -1]. Following the same logic, the full uptake release table become:

    uptakeReleaseTable =

    4×5 table

    Metabolite            Mean       Std      coefficients     fluxIdx 
    _________________    _______    ______    ____________    _________

    {'Glucose'      }    -39.015    4.2917      {[1 -1]}      {[ 28 1]}
    {'Lactate'      }     45.521    4.0969      {[1 -1]}      {[11 10]}
    {'Glycogen'     }    -16.809    2.0171      {[  -1]}      {[   26]}
    {'Ketone bodies'}     14.083    1.6899      {[   1]}      {[   20]}

This makes calculating the simulated net release fluxes fairly easy since for each row of the uptakeReleaseTable the value that is compared the data point is $\Delta \nu = coefficients * \nu (fluxIdx)$.

Now we almost have all the components we need to estimate the metabolic fluxes. The last thing we need is to look at how to run a simulation of the EMU model and by extension how we can set up an objective function for our flux estimation problem.

Task 5: Simulate the EMU model

Simulating the EMU model is actually fairly straight forward since there are no time dependent dynamics to be calculated. For a given flux vector $\nu$ we only need sequentially solve the EMU equation for each EMU network, for each EMU size. OpenFLUX2 configures the EMU equations based on the model definition into two matlab files in the model sub-folder. The matlab file loader_EMUModel defines the $A_{n,k}(\nu)$ matrices and calculates the inverted matrices $A_{n,k}^{-1}(\nu)$.

The file EMUModel contains the actual EMU equations such that

$X_{n,k} = A_{n,k}^{-1}(\nu) B_{n,k}(\nu) Y_{n,k}(y^{in},X_{n}, X_{n-1},...,X_{1})$

where $y^{in}$ are the substrate EMUs saved in the inputSubEMUX.mat files.

Running the EMUModel will result in all required EMUs being calculated and among them the target EUMs we want to compare to our simulated data. To help sort these out OpenFLUX2 also defined the script x_sim in the Model project folder. This small script structures the EMUs specified in the simulatedMDVs-list during the model definition into a single column vector. Thus, by calling x_sim after EMUModel we will obtain a variable x_calc that have all our simulated MIDs in the order specified by the "simulatedMDVs"-list.

Your task is to

Run a simulation of the EMU model for an input of your choice.
- Remember that you need to choose a suitable flux vector v.

Modify the x_sim-script

The x_sim-script essentially describes our measurement equation (What we typically call $\hat{y}$). Thus, if we want to modify the measurement equation x_sim is the place to modify. If we for instance want to change the structure of the simulated MIDs to put them in a different order to match our MID data, the easiest way is to manually modify the x_sim-script.

Metabolites across multiple compartments If we have metabolites across multiple compartments these will be defined as different metabolites in the model definition.

## simulatedMDVs
   # Pyr_C#111
   # Pyr_M#111

However, the MID measurements will likely represent some weighted combination of the MIDs across these different compartments thus we want to attach weights to each MID in x_sim. For the example here with Pyr_C and Pyr_M the entry for Pyr in the x_calc vector could be calculated as:

x_calc=[
(Pyr_C_111' + Pyr_M_111')./2
 ];

where the compartments "C" and "M" are assumed to be equally weighted, i.e. the measurement signal for Pry is assumed to originate in equal measure from the two compartments, and thus the resulting simulated MID for Pyr is the average of the MID for Pyr_C and Pyr_M. Note that Pyr_C_111 and Pyr_M_111, and all calculated MIDs, are row vectors and need to be transposed to fit into the column vector x_calc.

The scripts `build_X_sim_file` and `build_X_sim_file_weightedComps`¶

There are two scripts in the modified toolbox that automatically modifies the x_sim file. These are described in their respective boxes below for this exercise the using the script build_X_sim_file will suffice.

build_X_sim_file

There is a script in this toolbox called build_X_sim_file that automatically modifies the x_sim file such that metabolites with the same name are structured together with the resulting simulated MID is averaged across all compartments that metabolite appears in. To use build_X_sim_file simply run the script once form the matlab command line after the model compilation step. The script will print the new structure of x_sim to the command line. You can also check and correct any potential errors directly in the x_sim file.

build_X_sim_file

x_calc defined as:
x_calc = [
Gluc_B_111111'
(G6P_M_111111' + G6P_L_111111')./2
(Pyr_M_111' + Pyr_L_111')./2
Fum_L_1111'
(CO2_L_1' + CO2_M_1')./2
];

Note that metabolites that appear only in one compartment will remain unaltered e.g. Fum_L_1111'

build_X_sim_file_weightedComps

There is also a more advanced version of build_X_sim_file called build_X_sim_file_weightedComps. This script works in a similar fashion, modifying the x_sim script but instead of assuming metabolites should be averaged across departments this version introduces scaling parameters thetaScale. These parameters individually scale the contribution of each metabolite from each compartment, such that the sum of each metabolite across all compartments sums to 1. For instance, if G6P exists in three compartments and pyr exists in two compartments the resulting calculations for x_calc would be:

build_X_sim_file_weightedComps

x_calc defined as:
x_calc = [
Glucose_C_111111'
(thetaScale(1) .* G6P_C_111111' + thetaScale(2) .* G6P_M_111' + (1 - sum(thetaScale(1:2))) .* G6P_L_111111')
(thetaScale(3) .* Pyr_C_111' + (1 - thetaScale(3)) .* Pyr_M_111')
];

where thetaScale(1) and thetaScale(2) together determine the contributions of G6P from compartments "C", "M", and "L". While thetaScale(3) determines the contributions of Pry from compartments "C" and "M". Metabolites that appear only in one compartment will remain unaltered e.g. Glucose_C_111111'.

build_X_sim_file_weightedComps will in addition to modifying x_sim create the file nCompartmentScalingParameters.mat in the Model project folder. This file will contain four variables specific to the thetaScale parameters. These four variables are:

nEq_constraints - This is the number of equality constraints created by the thetaScale parameters. For instance, from the example above the parameters thetaScale(1) and thetaScale(2) cannot sum to more than 1 of the contribution from compartment "L" would be negative.
nScaleParameters - This is the total number of scaling parameters introduced i.e. the length of the vector thetaScale.
thetaScaleCoefficientIdx - This is a cell-array that maps which thetaScale parameters affect which metabolites e.g.

thetaScaleCoefficientIdx =

3×2 cell array

    {'Glucose'}    {0×0 double}
    {'G6P'    }    {[    1  2]}
    {'Pyr'    }    {[       3]}

The thetaScale parameters can be set manually or estimated via parameter estimation. Note that if the thetaScale parameters are estimated you must introduce constraints to ensure that the thetaScale-parameters that scale the same metabolite do not sum to more than 1. In the example above the following constraint would need to be introduced: $g_{i}(\theta) = \theta_1 + \theta_2 \le 1$

How to run a simulation of the EMU model

To simulate the EMU model we thus want to run the following sequence of commands for each labelling configuration, from the Model project folder

load('inputSubEMU1.mat')
loader_EMUModel
EMU_model
x_sim

The following code sequence will simulate the MIDs for the number of experiments determined by the variable nExperiments and store the simulated MIDs for all experiments in the variable MID_sim.

for j = 1:nExperiments

    load(sprintf('inputSubEMU%0.0f.mat',j)); % load the correct input tracer

    loader_EMUModel % load the A and A_inv matrices
    EMUModel % the EMU model depends on the flux vector v

    x_sim % simulated measurement vector x_calc

    finiteEntries = isfinite(x_calc);
    x_calc(finiteEntries==0) = 0;

    MID_sim{j} = x_calc;

end

Where j is a loop index variable to load the correct set of substrate EMUs. This order will be determined by the order of which the different configurations of substrate EMUs were defined.

Please note that the script loader_EMUModel require a vector v with the flux values. For this specific example, a viable initial flux vector v is a vector of 30 ones. In other words, all fluxes are assumed to be equal.

    v = ones(30,1);

Plot the MID data and Simulation

There is not to much too say about plotting agreement between the model simulation and data. There is not really anything within the OpenFLUX2 framework that would interfere with plotting the model simulation and data in a way you seem feasible. Below are two common approaches to plot agreement to MID data.

Plot comparison between individual simulated and measured mass isotopomers You can plot the comparison between individual simulated and measured mass isotopomers for each metabolite. This could for instance be done by plotting the measured and simulated MIDs as bar graphs for each metabolite.

Plot comparison between simulated and measured MIDs Since the total abundance of a metabolites mass isotopomers always sum to 1. The MIDs cam be plotted as stacked bar graphs where each stack sum to 1 and the relative abundance of different mass isotopomers are indicated by different colours. Thus simulated and measured MIDs for each metabolite can be compared. This provides a more space efficient way to plot the same information as above, with the exception that measurement uncertainty for individual mass istopomers are more difficult to accurately portray.

Plot an overall comparison between all simulated and measured MIDs Lastly, if we are only interested in the overall agreement between the model simulation and the measured data, we can plot the corresponding simulated and measured values as x and y points in a scatter graph. This graph will convey an overall illustration of the model fit. Points near the diagonal represent data points where there is good agreement between the model simulation and measured data. Points far from the diagonal are data points where the model has a poor fit. This is perhaps the most space efficient way to illustrate the model fig to a large data set. However, it is more difficult to evaluate which individual data points that the model might struggle to describe.

Note that the three figures above all illustrate the same data and model simulation.

If you want to use it the toolbox has a function for plotting multiple parallel MIDs and corresponding simulations. This function is called plotMIDsParallel(). This function uses the first of the options above.

plotMIDsParallel()

This function takes from three to six input argument. The three mandatory input arguments are 1. MID data - the MID data structured as a n-by-m cell array. Where n is the number of different MID data sets and m is the number of metabolites in each set. Each cell should contain the MID for the respective metabolite. These values will be plotted as m different bar charts. With n series of bars in each chart. 2. MID Error - the MID SEM or measurement error structured in a similar n-by-m cell array. These values will be plotted as error bars attached to the corresponding bar. 3. Simulated MIDs - the model simulated MIDs structured in the same n-by-m cell array. These values will be plotted as additional bars to the right of the corresponding data bar in a slightly brighter colour.

The next three input arguments are optional. 4. Metabolite Names - This should be a 1-by-m cell array containing the names of each metabolite in the form of a string. If not provided each bar chart will receive a numeric title from 1 to m. 5. Simulated MID error - the model uncertainty of the simulated MIDs. structured in a similar fashion as the MID Error as a n-by-m cell array. These values will be plotted as error bars on the corresponding simulated MID bar. 6. the figure number - An integer specifying if the figure should be plotted in a specific matlab figure. If not provided the next available Matlab figure will be used.

Example:

measured_MIDs =

    2×8 cell array

        {7×1 double}    {7×1 double}    {4×1 double}    {4×1 double}    {4×1 double}    {5×1 double}    {5×1 double}    {2×1 double}
        {7×1 double}    {7×1 double}    {4×1 double}    {4×1 double}    {4×1 double}    {5×1 double}    {5×1 double}    {2×1 double}


MID_error =

    2×8 cell array

        {7×1 double}    {7×1 double}    {4×1 double}    {4×1 double}    {4×1 double}    {5×1 double}    {5×1 double}    {2×1 double}
        {7×1 double}    {7×1 double}    {4×1 double}    {4×1 double}    {4×1 double}    {5×1 double}    {5×1 double}    {2×1 double}


simulated_MIDs =

    2×8 cell array

        {7×1 double}    {7×1 double}    {4×1 double}    {4×1 double}    {4×1 double}    {5×1 double}    {5×1 double}    {2×1 double}
        {7×1 double}    {7×1 double}    {4×1 double}    {4×1 double}    {4×1 double}    {5×1 double}    {5×1 double}    {2×1 double}


MetaboliteNames =

    1×8 cell array

        {'Glucose'}    {'G6P'}    {'G3p'}    {'Pyr'}    {'Lact'}    {'SucCoA'}    {'Fum'}    {'CO2'}

figureHandle = plotMIDsParallel(measured_MIDs, MID_error, simulated_MIDs, MetaboliteNames);

On final thing to consider before we set up an objective function is the concept of independent or "free" fluxes. Due to the stoichiometry of metabolic networks and the assumption that we are at a metabolic steady-state some flux values will be entirely determined by other fluxes in the system. Thus, the number of independent parameters in the system is less than the total number of fluxes.

Free fluxes

Since these types of metabolic networks are defined by a specific stoichiometry a stoichiometric matrices $S$ can be formulated. For the stoichiometric matrix $S$ the rows represent metabolites and columns represent reactions (fluxes). Since we also assume that the network is at metabolic a steady-state we introduce a conservation of mass requirement for each node of the network i.e. what goes into a node must come out of it. Thus, many of the fluxes are interconnected due to this conservation of mass, resulting in linearly dependent rows or columns in the $S$ matrix. Because of these interconnections, not all fluxes in the system can vary independently. Some fluxes are inherently defined by others due to the stoichiometry of the network. For example, in a simple two-reaction system where reaction 1 produces a metabolite that is then consumed by reaction 2, the fluxes of these reactions are not independent. If you know the flux of reaction 1 and there's no accumulation of the intermediary metabolite, the flux of reaction 2 is implicitly defined. This means that only a subset of all fluxes in the network are so-called independent or "free" fluxes.

Definition of Independent Fluxes: Independent fluxes are those that can vary freely without being inherently defined by the stoichiometry of other reactions in the network. They act as "free parameters" in the flux estimation process.

Please note that the configuration of the independent flux subset is not unique for a specific metabolic network. The number of independent fluxes is determined by the number of interconnections in the network stoichiometry, but which of the interconnected fluxes should be considered independent is not uniquely determined. The OpenFlux2 toolbox referees to the subset of independent fluxes as the "Flux Basis" and allows the user to set preferences for which parameters should be considered part of the independent flux subset. This is what the property "Basis" indicates during the model definition.

Example of free flux breakdown

To better understand how the flux configuration of a metabolic network can be reduced to an independent flux configuration, let us consider a simple network introduced by Antoniewicz et al., 2007. This network has 6 metabolites $A - F$ and 6 fluxes $\nu_1 - \nu_6$ and is depicted in the figure below.

Since we assume that the network is at metabolic steady-state all fluxes that goes into a node must be balanced by the fluxes coming out of that node. This means that we can write the relationship between the fluxes as shown to the right in the figure above.

However, we can also formally define the same relationships from the stoichiometry of the network. If we write the stoichiometric matrix for the intermediary metabolites $B$,$C$, and $D$ with the metabolites representing the rows and the fluxes representing the columns we get:

$\begin{matrix} B\\ C\\ D\\ \end{matrix}$ $\begin{bmatrix} 1 & -1 & 1 & -1 & -1 & 0 \\ 0 & 0 & 0 & 1 & -1 & 0\\ 0 & 1 & -1 & 0 & 1 & -1\\ \end{bmatrix} \implies$ $S=\begin{bmatrix} 1 & -1 & 1 & -1 & -1 & 0 \\ 0 & 0 & 0 & 1 & -1 & 0\\ 0 & 1 & -1 & 0 & 1 & -1\\ \end{bmatrix}$

We can also define the flux vector as a column vector:

$\nu = \begin{bmatrix} \nu_1 \\ \nu_2 \\ \nu_3 \\ \nu_4 \\ \nu_5 \\ \nu_6 \\ \end{bmatrix}$

The metabolic steady-state can thus be defined mathematically as

$S*\nu=0 \Leftrightarrow \begin{align} \nu_1 - \nu_2 + \nu_3 -\nu_4 - \nu_5 &= 0 \\ \nu_4 - \nu_5 &= 0 \\ \nu_2 - \nu_3 + \nu_5 - \nu_6 &= 0 \\ \end{align} \Leftrightarrow$ $\begin{align} \nu_1 + \nu_3 &= \nu_2 + \nu_4 + \nu_5 \\ \nu_4 &= \nu_5 \\ \nu_5 + \nu_2 &= \nu_3 + \nu_6 \\ \end{align}$

We can now see that this definition based on the network stoichiometry matches the intuitive balancing of in and out fluxes.

Finally, by observing these flux relationships we can note that there are certain linear dependencies between the fluxes. For example we could rewrite these relationships as:

$\begin{align} \nu_2 &= \nu_1 + \nu_3 - 2*\nu_4 \\ \nu_5 &= \nu_4 \\ \nu_6 &= \nu_1 - \nu_4\\ \end{align}$

in other words we can express fluxes $\nu_2$, $\nu_5$, and $\nu_6$ in terms of $\nu_1$, $\nu_3$, and $\nu_4$. In this case we would call $\nu_1$, $\nu_3$, and $\nu_4$ the independent of free fluxes as all other fluxes in the network can be determined from these fluxes.

Please note that ,as stated above, there is no one unique independent flux configuration. For this example we can define an equally valid independent flux configuration by rewriting the flux relationships as:

$\begin{align} \nu_1 &= - \nu_6 - \nu_5 \\ \nu_4 &= \nu_5 \\ \nu_3 &= \nu_2 +\nu_5 - \nu_6\\ \end{align}$

Now $\nu_1$, $\nu_3$, and $\nu_4$ are determined in terms of the independent fluxes $\nu_2$, $\nu_5$, and $\nu_6$.

From a computational perspective, the existence of independent fluxes means that there are fewer free parameters that determine the systems output, i.e. fewer parameters that needs to be estimated. However, to calculate the full flux vector from the independent flux vector we need to calculate the stoichiometry matrix's $S$ null space matrix $N$. If we assume that we are at a metabolic steady-state, which we do. we will have the following relation between the stoichiometric matrix $S$ and the full flux vector $\nu$.

$S\cdot \nu=0$

i.e. the sum of all fluxes that produces and consumes each metabolite equals 0. $S$ will be an m-by-k matrix for a network with m metabolites and k fluxes. The null space of matrix $S$ is the set of all solutions to the homogeneous equation $Sx=0$. There is in general not one unique null space for a given matrix. Although, since we know the number of free fluxes, from knowing $S$ we can calculate a flux vector $\nu$ that fulfils the stoichiometric balance by solving.

$\nu = N\cdot u$

where $u$ is the vector of free independent fluxes. $N$ sill be a k-by-n matrix where n is the number of independent fluxes.

OpenFLUX2 has a script for calculating the null space matrix called define_ns, which is required for compatibility of various other functions in the toolbox.

define_ns

This Matlab script defines the null space matrix ns and a few additional important flux configuration variables that are required for various other functions. To run the define_ns script ensure that the current directory is the Model project folder and that the relevant /model-folder is added to path.

define_ns will create a few different variables, the most important is the variable modelFluxConfig. This variable contains some important flux configuration variables in the form of a matlab structure. These flux configuration variables are model specific and determined by the model definition, define_ns will also save the modelFluxConfig variable to the modelFluxConfig.mat-file.

Task 6: Define an objective function

To be able to estimate the metabolic fluxes as parameters we need to formulate an objective function that considers the MID data from all experiments we want to estimate simultaneously, the relevant uptake/release measurements, and any constraints that apply to the parameter configuration.

The objective function should receive the following input arguments

The free flux parameters $u$.
The structure containing the MID data.
The information of which experiment correspond to the respective inputSubEMUx.mat-file
The structure containing the uptake/release data.
The model flux configuration saved in modelFluxConfig/modelFluxConfig.mat-file.

The objective function should:

Calculate the full flux vector $\nu$ from the free flux vector $u$.
Simulate the EMU model for the calculated flux vector $\nu$.
Ensure that the simulation fulfils all constraints, such as flux balance constraints.
- Depending on your choice of optimisation solver you might need to implement a penalty function.
Calculate the weighted sum of squared residuals with respect to both the MID data and the uptake/release data.

The toolbox has functions for calculating the full flux vector $\nu$ from the free flux vector $u$.

How to use fluxCalc()

The function fluxCalc can be used to calculate the negative flux vector $-\nu$ from the independent flux vector $u$ i.e.

    v = -fluxCalc(u,modelFluxConfig)

The variable modelFluxConfig is an optional input argument but if modelFluxConfig is not provided fluxCalc() runs define_ns which is computational inefficient, especially during parameter estimation. The output being the negative flux vector $-\nu$ might seem unintuitive but is required for other parts of the OpenFLUX2 toolbox, thus remember to add a "$-$"-sign what using fluxCalc() to calculate the fluxes.

Additionally, fluxCalc() might result in some numerical instability for fluxes that are close to 0. Thus, resulting in elements that technically are less than 0 e.g. - 1e-14. To avoid this causing computational problems, we can set all fluxes with a value very close to 0 to be exactly 0.

In the case that we have any fluxes that are defined as reaction type "S" or "SF" during the model definition the activity of these fluxes will also need to be accounted for. For this we want to use the function appendSyn(). This function takes as inputs the flux vector v, the free flux vector u, and the model flux configuration modelFluxConfig, adn returns the modified flux vector v

In total to accurately calculate the flux vector $\nu$ from the independent flux vector $u$ we should have something similar to the following code:

    %% get flux vector v from free fluxes u
    v = - fluxCalc(u,modelFluxConfig); %calculate the full flux vector from the free fluxes
    v(abs(v)<1e-8)=0; % set numerically small values to zero
    v = appendSyn(v,u,modelFluxConfig); % needed if any fluxes are defined as types "S" or "SF".

OpenFLUX2 also has a function for formulating the non-linear constraints posed by the flux estimation problem. The function nonlcon() returns two vectors. The first represent the non-equivalent constraints i.e. $g_{i}(u) \le 0$, the second output represent the equivalent constraints i.e. $g_{i}(u) = 0$. Note that the non-equivalent constraints are used to ensure only non-negative fluxes $-\nu(u) \le 0 \iff \nu(u) \ge 0$. The equivalent constraints are used to ensure the stoichiometric balance i.e., $S*\nu = 0$.

nonlcon()

nonlcon() takes three input arguments: 1. u - The free flux vector. 2. constraints_e - a cell-array that OpenFLUX2 uses to specify any potential flux equivalent constraints. 3. modelFluxConfig - the model flux configuration structure.

Thus to calculate the non-linear constraints for an independent flux vector u call nonlcon such that:

    [v_noneq, v_eq] = nonlcon(u,constraints_e,modelFluxConfig);

Exactly how optimization constraints are implemented depends on the exact algorithm/solver used and will not be covered here. But to fulfil the model's constraints the variables v_noneq and v_eq should fulfil:

    v_noneq <= 0;
    v_eq = 0;

constraints_e The variable constraints_e is a cell-array that OpenFLUX2 uses to specify any potential flux equivalence constraints, e.g. $\nu(1) = \nu(2) \iff \nu(1)-\nu(2) = 0$. If no such constraints should be placed on the flux vector constraints_e should be empty constraints_e = []. Otherwise, constraints_eshould be defined as text strings in cells such as:

    constraints_e =

    1×2 cell array

        {'v(1)-v(2)'}    {'v(3)-v(2)'}

Each cell should contain a unique flux equivalence constraint.

The function setFluxEqualityConstraints() can be used to generate constraints_e. The function requires no input arguments and will prompt the user to enter the flux equality constraints.

At long last we have everything we need to start the flux estimation process. This exercise will assume that you are familiar with the core concepts of parameter estimation, parameter uncertainties, and model uncertainties and thus will not explain these concepts any further. These concepts generally remain the same when applied to ¹³ C MFA. Some slight complications arise from the fact that the estimated parameters constitute a subset of the model parameters (Independent fluxes vs all fluxes) and the stoichiometric constraints.

Task 7: Run a parameter estimation

Use a parameter estimation approach of your choice to:

Evaluate the fluxes for the two experiments with healthy condition, simultaneously.
Evaluate the fluxes for the diabetic conditions experiment.

One thing to note is that the lower and upper bounds (lb and ub) for the fluxes $\nu$ are not necessarily the same as lb and ub for the for the independent fluxes $u$. Considering a small extraction from an example model, we have a situation where $\nu_1 = 2*u_1-2*u2$ even if we have the lb and ub of $lb = 0 \le \nu_1 \le 1 = ub$ there is actually an infinite amount of values for $u_1$ and $u_2$ that satisfies these conditions i.e.

$u_2 \le u_1$

$u_1 \le u_2 + \frac{1}{2}$

Now in practice $u_1$ and $u_2$ are probably further constrained by additional flux dependencies but this example serves to show that we cannot assume that if we set $lb$ and $ub$ conditions for $\nu$ that will correspond to the same $lb$ and $ub$ for $u$. Note that the opposite is also true, that $lb_u \neq lb_{\nu}$ and $ub_u \neq ub_{\nu}$

We can use the getFreeFluxLBandUB-function to get the $lb_u$ and $ub_{u}$ from $lb_{\nu}$ and $ub_{\nu}$.

getFreeFluxLBandUB

The function takes $lb_{\nu}$ and $ub_{\nu}$ as input arguments in the form of scalar values. Additionally, the modelFluxConfig variable is required. Optional input arguments are the upper and lower bounds for reversible reactions. For example.

lb_v = 0;
ub_v = 1e3;

rev_lb = 0;
rev_ub = 1e2;

[lb,ub] = getFreeFluxLBandUB(lb_v, ub_v, modelFluxConfig, rev_lb, rev_ub)

The outputs lb and ub will be vectors with the length corresponding to the number of independent fluxes.

Note that having different bounds for forward and reversible fluxes might be useful to prevent very large parameter values that are really constrained with respect to a net flux through the reaction. For example, suppose that we have $[lb, ub] = [0, 1000]$ and most flux values might have values around 10-20. An unbounded reversible flux would likely result in the forward and reverse flux having values of $\nu_F = 998$ and $\nu_R = 989$ respectively. This means that the net flux $\nu_F - \nu_R = 9$ which is in the same magnitude as the other fluxes but the range across the flux vector is numerically very large. This in turn might make the results more difficult to interpret.

For similar reasons as setting $lb$ and $ub$ for the independent fluxes, it is not entirely straight forward finding a suitable start guess for the parameter estimation. The main complication lies in finding a start guess $u_0$ that satisfies the flux balancing constraints (and potential flux equality constraints). We could of course start with a random vector within the boundary conditions and allow the optimisation algorithm to find a solution that satisfies the constraints. However, this approach risks being quite computationally inefficient since a random point in the solution space could be very far from the acceptable constrained solution space. Alternatively, we could use the function getRandomX0()to generate an initial parameter vector that at least satisfies the constraints.

How to use getRandomX0()

The getRandomX0()-function takes four input arguments.

lb - the lower bounds for the independent fluxes $u$.
ub - the upper bounds for the independent fluxes $u$.
modelFluxConfig - the model flux configuration generated by define_ns. This argument is optional, if not provided the function will run define_ns to generate the modelFluxConfig structure.
Mode - This should be an integer 1 or 2. The input switches the approach for finding the initial parameter vector. Mode 1 is OpenFLUX2's default way of selecting an initial parameter vector. Mode 2 is an alternative self-made approach which is faster but less tested. This input is optional, and the function will default to mode 1.

u0 = getRandomX0( lb, ub,modelFluxConfig,2);

The function returns an independent flux vector that satisfies the constraints. Note that the function might take a few seconds to find a suitable vector for either mode.

To summarize¶

Here we now put together all the different tasks of this exercise and thus I want to shortly summaries what should be done before an optimization algorithm is initiated to ensure success. Please make sure that you have:

imported, structured, and loaded the MID data and the substrate EMUs in a good way (Task 3).
imported, structured, and loaded the uptake/release data in a good way (Task 4).
set the current directory to the Model project folder. e.g. cd(['./Models/',modelName]).
run the define_ns- script to generate the modelFluxConfig-variable
suitable upper and lower bounds ($ub$ and $lb$) for the independent fluxes.
configured the relevant number of model constraints.
an Objective function that returns a scalar value for the quantitative agreement between model simulation and both the MID data and the uptake/release data. (Task 6)

This concludes this computer exercise and hopefully you have gained some more insights into the computational aspects of ¹³C MFA. Of course, a comprehensive project using ¹³C MFA would likely include multiple parameter estimations, comparisons between different experimental conditions, model reformulation, evaluation of the flux confidence intervals (identifiability analysis) etc. But these concepts are not unique to ¹³C MFA and are thus not covered by this exercise. Below are some descriptions of a few additional functions that are currently part of the modified toolbox.

For PhD students to pass this course you should submit a short report where you present the result of the implementation of the Glucose metabolism model used in this computer exercise. The report should be 2-3 pages in length (including figures) where you present a successful implementation of the model and a fit to the MID and uptake release flux data. You should also present what flux estimates you obtained for the healthy and diabetic conditions respectively and if you could determine any significant differences in fluxes between the two conditions.

Other potentially useful toolbox functions

buildModelStoichiometry()

This function takes no input arguments and returns two cell arrays with the model's metabolite stoichiometry and flux dependencies written out as strings. The metabolite stoichiometry specifies how each intermediary metabolite (i.e. no substrates or products) are affected by each flux. Note that this information is is the stoichiometric matrix $S$ with any 0 elements removed. The second output, the flux dependencies specify how each flux $\nu_i$ depends on the independent fluxes $u_i$. This function is very useful to get a better understanding for how the model is constructed and how to translate from the independent fluxes to fluxes to metabolites.

The function should be called from the Model project folder.

[MetaboliteStoichiometry, fluxDependencies] = buildModelStoichiometry()

MetaboliteStoichiometry =

    3×1 cell array

        {'B = + v(1) - v(2) + v(3) - v(4) - v(5)'}
        {'C = + v(4) - v(5)'                     }
        {'D = + v(2) - v(3) + v(5) - v(6)'       }


fluxDependencies =

    6×1 cell array

        {'v(1) = + 1.00 * u(2) '                            }
        {'v(2) = + 1.00 * u(1) + 1.00 * u(2) - 2.00 * u(3) '}
        {'v(3) = + 1.00 * u(1) '                            }
        {'v(4) = + 1.00 * u(3) '                            }
        {'v(5) = + 1.00 * u(3) '                            }
        {'v(6) = + 1.00 * u(2) - 1.00 * u(3) '              }

exportFluxResults2txtFile

This function exports a flux vector v to a txt file. the function takes two inputs:

modelFileName - a text string with the name of the model tab-delimited text file.
v - the flux vector that should be exported.

The function yields no output but creates a file named FluxResults.txt with the name of each flux (from the model definition) and the exported flux value.

>> exportFluxResults2txtFile(modelFileName.txt,v)


FluxResults.txt
----------------
v1  40.5376273682509
v2  45.5342659123496
v3  25.8260266919871
...

exportMIDsimulation2txtFile

This function simulates the MIDs for a given flux vector v and exports the simulated MIDs to a text file names MIDResults_[modelName].txt. The function takes the following input arguments:

SubstrateInfo - the substrateInfo cell-array with the substrate atom enrichment information.
modelName - a text string with the model name.
v - the full flux vector for which to simulate the MIDs.
outputOption - this is a string that reads either full or part. This argument specifies if the exported MIDs should contain all model simulated MIDs (full) or just the MIDs for the metabolites specified in the "simulatedMDVs"-list in the model definition.

>> exportMIDsimulation2txtFile(substrateInfo, 'modelName', v, 'full')

MIDResults_[modelName].txt
---------------------------
AcCoA-L 0   0.757821304129669   0
AcCoA-L 1   0.0569750612046194  0
AcCoA-L 2   0.185203634665711   0
CO2-L   0   0.827167872965776   1
CO2-L   1   0.172832127034224   1
CO2-M   0   0.437998698187812   1
....

The exported information is structured in four columns (tab-delimited). The first column specifies the metabolite names. Note that in this export is the raw MIDs i.e. before any weighting of compartments is done by the x_sim measurement equation, hence all metabolites are listed from all compartments. The second column specifies the mass isotopomer. The third column contains the simulated MID value. The last column contains a boolean value (1 or 0) that specifies if the metabolite is listed in the "simulatedMDVs"-list or not.

exportModel2GraphNetwork

Takes one input argument that is the filename that is the model tab-delimited text file. The function returns a directed graph (digraph) object that can be plotted as demonstrated in the example below. The function will also export the directed graph to an excel file named graphExport.xlsx. The graph network will have a node for each metabolite and each flux. For instance, if metabolite A becomes metabolite B via flux v1 that would be three notes with two edges i.e. A -> v1 -> B. Please note that executing the function might take a while. The model file needs to be on the current matlab search path.

[GraphHandel] = exportModel2GraphNetwork(fileName.txt)

plot(GraphHandel,'NodeLabel',GraphHandel.Nodes.Names)

exportThetaScale

This function is used to export the mixing model for the compartment weighted measurement equation constructed by build_X_sim_file_weightedComps. Running build_X_sim_file_weightedComps will yield a variable called outputString, that contains a cell array with the strings that are printed out by the build_X_sim_file_weightedComps-script. These strings specify which scaling parameter scales which compartmental contribution from which metabolite.

The function exportThetaScale() essentially exports this string with the thetaScale(x) parts replaced by numerical values. This function is useful to communicate the estimated contributions from different compartments. The function takes two inputs:

-inputString - This is the cell-array with the outputString from build_X_sim_file_weightedComps -thetaScale - The vector with the scaling parameters.

inputString =

    10×1 cell array

        {'x_calc = ['                                                             }
        {'Gluc_B_111111''                                                         }
        {'(thetaScale(1) .* G6P_M_111111' + (1 - thetaScale(1)) .* G6P_L_111111')'}
        {'(thetaScale(2) .* G3P_M_111' + (1 - thetaScale(2)) .* G3P_L_111')'      }
        {'(thetaScale(3) .* Pyr_M_111' + (1 - thetaScale(3)) .* Pyr_L_111')'      }
        {'Lact_B_111''                                                            }
        {'SucCoA_L_1111''                                                         }
        {'Fum_L_1111''                                                            }
        {'(thetaScale(4) .* CO2_L_1' + (1 - thetaScale(4)) .* CO2_M_1')'          }
        {'];'                                                                     }

[output] = exportThetaScale(inputString, [0.3 0.5 0.1 0.7])

output =

    8×1 cell array

        {'Gluc_B'                             }
        {'(0.3 .* G6P_M + (1 - 0.3) .* G6P_L)'}
        {'(0.5 .* G3P_M + (1 - 0.5) .* G3P_L)'}
        {'(0.1 .* Pyr_M + (1 - 0.1) .* Pyr_L)'}
        {'Lact_B'                             }
        {'SucCoA_L'                           }
        {'Fum_L'                              }
        {'(0.7 .* CO2_L + (1 - 0.7) .* CO2_M)'}

The function returns the inputString but with the thetaScale(x) replaced by the numerical values specified by the second input. The function also writes this output-string to a text file called mixingModel.txt.

getModelFluxNames

This function takes the name of a model text file and returns a cell array containing the name of all fluxes defined in the model, i.e. the names specified in the Flux Id column. The input argument is the file name of the model text file as a string.

[fluxNames] = getModelFluxNames(modelFileName)

fluxNames =

    30×1 cell array

        {'v1'}
        {'v2'}
        {'v3'}
        {'v4'}
        ...

reverseFluxCalc

This function is meant to be a reversed calculation of the fluxCalc()-function. In other words, reverseFluxCalc transforms a flux vector $\nu$ to an independent flux vector $u$. However, due to the nature of the null space matrix, there is no one unique independent flux vector $u$ for each flux vector $\nu$. As such this function only creates an approximation of which $u$ resulted in the provided flux vector $\nu$.

The function takes two input arguments: - v - the flux vector to be reduced to an independent flux vector. - modelFluxConfig - the model flux configuration structure. This input is optional and if not provided the function runs the define_ns-script.

[u,majorDiffIndx] = reverseFluxCalc(v,modelFluxConfig)

The function returns two outputs, the approximate of an independent flux vector u and a vector indicating the indices of the fluxes v(i) where there will have major difference (> 1e-6) between v and -fluxCalc(u). In other words, the fluxes where the approximation was not perfect.

Flux Solutions.

I acquired the following flux values when doing an parameter estimation using the MEIGO optimisation package with the enhances scatter search (ess) global algorithm and the ´fmincon´ local solver.

Please note that this is the solution I found and there might be other equally viable solutions.

Fluxes	Healthy condition	Diabetic condition
$\nu_1$	47.7975415039691	125.236483553118
$\nu_2$	61.6126481087393	76.9984201236403
$\nu_3$	35.8424862161597	51.0700950441123
$\nu_4$	77.3104856777391	77.7849752385841
$\nu_5$	25.7701618925797	25.928325079528
$\nu_6$	25.7701618925797	25.928325079528
$\nu_7$	25.7701618925797	25.928325079528
$\nu_8$	97.455134324899	128.068515167753
$\nu_9$	97.455134324899	128.068515167753
$\nu_{10}$	20.5391874970854	0.00107307514183818
$\nu_{11}$	66.6741455651112	37.2024082793486
$\nu_{12}$	51.3201762568732	90.8671799635459
$\nu_{13}$	9.52496835378137	99.5736846716067
$\nu_{14}$	41.7952475286679	0.00391197797168214
$\nu_{15}$	18.8914241121496	995.997474002442
$\nu_{16}$	18.8914241121496	995.997474002442
$\nu_{17}$	54.8975510399741	1992.89178624011
$\nu_{18}$	36.0061269278244	996.894312237671
$\nu_{19}$	5.93948829182959	997.320232541201
$\nu_{20}$	14.4216558541739	0.663335258365407
$\nu_{21}$	9.52496835378137	99.5736846716067
$\nu_{22}$	9.52492872820532	90.8632679855742
$\nu_{23}$	3.96255760577446e-05	8.71041668603256
$\nu_{24}$	4.77700941953757	111.302938044739
$\nu_{25}$	7.15096907387144	101.083103015157
$\nu_{26}$	16.5124285835069	55.5958963741949
$\nu_{27}$	23.6633976573783	156.678999389351
$\nu_{28}$	9.8482910526081	204.917062818829
$\nu_{29}$	77.3104856777391	77.7849752385841
$\nu_{30}$	89.1030641067485	2091.57254465446

The exact values can be downloaded here

The flux solution for the healthy condition above is fitted to the MID data from both the healthy-glucose and the healthy-lactate tracer experiments simultaneously. As well as the uptake release fluxes for the health condition. This means that the model is fitted to a total of $(38*2)+4 = 80$ data points.

The flux solution for the diabetic condition is fitted to the MID data from the diabetic-glucose tracer experiment. As well as the uptake release fluxes for the diabetic condition. This means that the model is fitted to a total of $(38)+4 = 42$ data points.

The objective function value for the fit of the healthy condition is: 98.94.

The objective function value for the fit of the diabetic condition is: 48.00.

Flux	Reaction	Atom mapping	Compartment
\(v_1\)	Glucose Source -> Glucose	abcdef -> abcdef	Source -> Blood
\(v_2\)	Glucose -> G6P	abcdef -> abcdef	Blood -> Muscle
\(v_3\)	G6P -> 2x G3P	abcdef -> cba + def	Muscle
\(v_4\)	G6P -> R5P CO2	abcdef -> bcdef + a	Muscle
\(v_5\)	2x R5P -> S7P + G3P	abcde + ABCDE -> abABCDE + cde	Muscle
\(v_6\)	S7P + G3P -> G6P+ E4P	abcdefg + ABC -> abcABC + defg	Muscle
\(v_7\)	R5P + E4P -> G6P + G3P	abcde + ABCD -> abABCD + cde	Muscle
\(v_8\)	G3P -> Pyr	abc -> abc	Muscle
\(v_9\)	Pyr -> Lac	abc -> abc	Muscle -> Blood
\(v_{10}\)	Lac Source -> Lac	abc -> abc	Source -> Blood
\(v_{11}\)	Lac -> Lac Output	abc -> abc	Blood -> Output
\(v_{12}\)	Lac -> Pyr	abc -> abc	Blood -> Liver
\(v_{13}\)	Pyr + HCO3 source -> OAC	abc + A -> abcA	Liver
\(v_{14}\)	Pyr + CoA -> AcCoA + CO2	abc + X -> ab + c	Liver
\(v_{15}\)	OAC + AcCoA -> SucCoA + 2x CO2	abcd + AB -> ABbc + a + d	Liver
\(v_{16}\)	SucCoA -> Fum	abcd -> abcd	Liver
\(v_{17}\)	Fum -> OAC	abcd -> abcd	Liver
\(v_{18}\)	OAC -> Fum	abcd -> abcd	Liver
\(v_{19}\)	FA Source -> AcCoA	ab -> ab	Liver
\(v_{20}\)	2x AcCoA -> Ketone	ab + AB -> abAB	Liver
\(v_{21}\)	OAC -> PEP + CO2	abcd -> abc + d	Liver
\(v_{22}\)	PEP -> G3P	abc -> abc	Liver
\(v_{23}\)	PEP -> Pyr	abc -> abc	Liver
\(v_{24}\)	Glycerol Source -> G3P	abc -> abc	Liver
\(v_{25}\)	2x G3P -> G6P	abc + ABC -> cbaABC	Liver
\(v_{26}\)	Glycogen Source -> G6P	abcdef -> abcdef	Liver
\(v_{27}\)	G6P -> Glucose	abcdef -> abcdef	Liver -> Blood
\(v_{28}\)	Glucose -> Glucose Output	abcdef -> abcdef	Blood -> Output
\(v_{29}\)	CO2 -> CO2 Output	a -> a	Muscle-> Output
\(v_{30}\)	CO2 -> CO2 Output	a -> a	Liver -> Output

Fluxes	Healthy condition	Diabetic condition
\(\nu_1\)	47.7975415039691	125.236483553118
\(\nu_2\)	61.6126481087393	76.9984201236403
\(\nu_3\)	35.8424862161597	51.0700950441123
\(\nu_4\)	77.3104856777391	77.7849752385841
\(\nu_5\)	25.7701618925797	25.928325079528
\(\nu_6\)	25.7701618925797	25.928325079528
\(\nu_7\)	25.7701618925797	25.928325079528
\(\nu_8\)	97.455134324899	128.068515167753
\(\nu_9\)	97.455134324899	128.068515167753
\(\nu_{10}\)	20.5391874970854	0.00107307514183818
\(\nu_{11}\)	66.6741455651112	37.2024082793486
\(\nu_{12}\)	51.3201762568732	90.8671799635459
\(\nu_{13}\)	9.52496835378137	99.5736846716067
\(\nu_{14}\)	41.7952475286679	0.00391197797168214
\(\nu_{15}\)	18.8914241121496	995.997474002442
\(\nu_{16}\)	18.8914241121496	995.997474002442
\(\nu_{17}\)	54.8975510399741	1992.89178624011
\(\nu_{18}\)	36.0061269278244	996.894312237671
\(\nu_{19}\)	5.93948829182959	997.320232541201
\(\nu_{20}\)	14.4216558541739	0.663335258365407
\(\nu_{21}\)	9.52496835378137	99.5736846716067
\(\nu_{22}\)	9.52492872820532	90.8632679855742
\(\nu_{23}\)	3.96255760577446e-05	8.71041668603256
\(\nu_{24}\)	4.77700941953757	111.302938044739
\(\nu_{25}\)	7.15096907387144	101.083103015157
\(\nu_{26}\)	16.5124285835069	55.5958963741949
\(\nu_{27}\)	23.6633976573783	156.678999389351
\(\nu_{28}\)	9.8482910526081	204.917062818829
\(\nu_{29}\)	77.3104856777391	77.7849752385841
\(\nu_{30}\)	89.1030641067485	2091.57254465446

Introduction to modelling for 13C metabolic flux analysis (MFA)¶

Theoretical background¶

Practical computer exercise¶

The scripts build_X_sim_file and build_X_sim_file_weightedComps¶

To summarize¶

The scripts `build_X_sim_file` and `build_X_sim_file_weightedComps`¶