Model formulation exercises

1. Formulating equations from interaction graphs and reactions

In this section you will define mathematical equations for ODE models from interaction graphs.

1.1 A simple system

We have the system illustrated below, represented as an interaction graph, where all reactions are with mass action kinetics.

Note that ∅ here represent "nothing", and is meant to show that \(B\) and \(C\) are being degraded/removed over time. ∅ is not considered a state. Also note that arrows pointing at reactions correspond to that the state has an effect on the reaction, but is itself not being used for the reaction.

Questions

1. List all model states
2. For the system, what are the reaction rates? Introduce parameters as needed.
3. What are the ODEs? Reuse your reaction rates.
4. Assume that we can measure something proportional to \(B\). Give such a measurement equation.
5. Let's assume that the reaction \(A \rightarrow B\) instead is saturated with respect to A. How would the equations change?
6. What would happen to \(A\), \(B\) and \(C\) after a long time?

Detailed answers

1. List all model states

The model states are the components of the model that vary over time. In this model, the states are \(A\), \(B\) and \(C\).

2. For the system, what are the reaction rates? Introduce parameters as needed.

Let's refer to the reaction rates for reaction \(A \rightarrow B\) as \(v1\), \(B \rightarrow A\) as \(v2\), \(B \rightarrow ∅\) as \(v3\), \(B \rightarrow C\) as \(v4\), and \(C \rightarrow ∅\) as \(v5\).

We know that the reaction rates are of mass action kinetics, thus all reaction rates will correspond to a kinetic rate parameter multiplied by the state the reaction is originating from. Thus we get:

\[ \begin{align} &v1 = k1 \cdot A \\ &v2 = k2 \cdot B \cdot C \\ &v3 = k3 \cdot B \\ &v4 = k4 \cdot B \\ &v5 = k5 \cdot C \end{align} \]

Since we have introduced parameters (\(k1\), \(k2\), \(k3\), \(k4\), \(k5\)) we should give them some arbitrary values. Let \(k1=1\), \(k2 = 1\), \(k3 = 2\), \(k4 = 5\), \(k5 = 2\).

3. What are the ODEs? Reuse your reaction rates. Introduce initial conditions as needed.

We can see that \(A\) is being depleated with the rate \(v1\), and refilled with the rate \(v2\). We can also see that \(B\) is being refilled with the rate \(v1\), and is being depleated with the rates \(v2\), \(v3\), and \(v4\). Furthermore, \(C\) is being refilled with the rate \(v4\) and depleated with the rate \(v5\). Thus, the ODEs for \(A\) \(B\), and \(C\) would be:

\[ \begin{align} &d/dt(A) = -v1 + v2\\ &d/dt(B) = v1 - v2 -v3 -v4\\ &d/dt(C) = v4 - v5 \\ \\ &A(0) = 10\\ &B(0) = 0\\ &C(0) = 15 \end{align} \]

The full system would be:

\[ \begin{align} &d/dt(A) = -v1 + v2\\ &d/dt(B) = v1 - v2 -v3 -v4\\ &d/dt(C) = v4 - v5\\ \\ &v1 = k1 \cdot A \\ &v2 = k2 \cdot B \cdot C \\ &v3 = k3 \cdot B \\ &v4 = k4 \cdot B \\ &v5 = k5 \cdot C \\ \\ &k1 = 1 \\ &k2 = 1 \\ &k3 = 2 \\ &k4 = 5 \\ &k5 = 2 \\ \\ &A(0) = 10\\ &B(0) = 0\\ &C(0) = 15 \end{align} \]

And optionally, the equations can also be given in the opposite order, starting with the parameters and ending with the ODEs:

\[ \begin{align} &k1 = 1 \\ &k2 = 1 \\ &k3 = 2 \\ &k4 = 5 \\ &k5 = 2 \\ \\ &A(0) = 10\\ &B(0) = 0\\ &C(0) = 15 \\ \\ &v1 = k1 \cdot A \\ &v2 = k2 \cdot B \cdot C \\ &v3 = k3 \cdot B \\ &v4 = k4 \cdot B \\ &v5 = k5 \cdot C \\ \\ &d/dt(A) = -v1 + v2\\ &d/dt(B) = v1 - v2 -v3 -v4\\ &d/dt(C) = v4 - v5 \end{align} \]

4. Assume that we can measure something proportional to \(B\). Give such a measurement equation.

Since we measure something proportional to \(B\), we need to introduce a new parameter (with an arbitrary value). Let \(ky = 5\). The measurement equation would then be \(\hat{y} = ky \cdot B\).

5. Let's assume that the reaction \(A \rightarrow B\) instead is saturated with respect to A. How would the equations change?

We need to change \(v1\) to have Michaelis-Menten kinetics. For this, we need to introduce two new parameters \(Km\) and \(Vmax\) (and remove the old \(k1\)). The reaction rate should be saturated with respect to A. Thus, the equation should be: \(v1 = Vmax \cdot A/(Km+A)\). Let \(Vmax = 2\), \(Km = 3\).

6. What would happen to \(A\), \(B\) and \(C\) after a long time?

Since there is no influx to the system and there is an outflow/degradation on \(B\) and \(C\), \(A\), \(B\) and \(C\) will eventually all depleat and go to 0.

Short answers

1. List all model states

\(A\), \(B\) and \(C\).

2. For the system, what are the reaction rates? Introduce parameters as needed.

\[ \begin{align} &v1: \quad A \rightarrow B \\ &v2: \quad B \rightarrow A \\ &v3: \quad B \rightarrow ∅ \\ &v4: \quad B \rightarrow C \\ &v5: \quad C \rightarrow ∅ \\ \\ &v1 = k1 \cdot A \\ &v2 = k2 \cdot B \cdot C \\ &v3 = k3 \cdot B \\ &v4 = k4 \cdot B \\ &v5 = k5 \cdot C \\ \\ &[k1, k2, k3, k4, k5]=[1, 1, 2, 5, 2] \end{align} \]

3. What are the ODEs? Reuse your reaction rates. Introduce initial conditions as needed.

\[ \begin{align} &d/dt(A) = -v1 + v2\\ &d/dt(B) = v1 - v2 -v3 -v4\\ &d/dt(C) = v4 - v5 \\ \\ &[A(0), B(0), C(0)] = [10, 0, 15] \end{align} \]

4. Assume that we can measure something proportional to \(B\). Give such a measurement equation.

\[ \begin{align} &\hat{y} = ky \cdot B\\ &ky = 5 \end{align} \]

5. Let's assume that the reaction \(A \rightarrow B\) instead is saturated with respect to \(A\). How would the equations change?

\[ \begin{align} &v1 = Vmax \cdot \frac{A}{Km+A} \\ &[Vmax, Km] = [2, 3] \end{align} \]

6. What would happen to \(A\), \(B\) and \(C\) after a long time?

\(A\), \(B\) and \(C\) will depleat and go to 0, since \(B\) and \(C\) is being removed, and there is no influx to the system.

1.2 Equations from reactions

Consider the following reactions

\[ \begin{align} & \text{Reaction 1}: \quad A \rightarrow B \\ & \text{Reaction 2}: \quad B \rightarrow C \\ & \text{Reaction 3}: \quad C \rightarrow \varnothing \\ \end{align} \]

Questions

1. List all model states
2. Write down the differential equations that corresponds to these reactions. Assume mass action kinetics for reaction 1 and 2 and assume that reaction 3 is saturated with respect to the concentration of C. Introduce parameters and initial conditions with values of your choice.
3. Add a measurement equation that states that you can measure the sum of the concentration of B and C.

Answers

1. List all model states

\(A\), \(B\), \(C\)

2. Write down the differential equations that corresponds to these reactions

\[ \begin{align} & \dot{A} = -k1 \cdot A & A(0) = 1 \\ & \dot{B} = -k2 \cdot B + k1 \cdot A & B(0) = 2 \\ & \dot{C} = -\frac{Vmax \cdot C}{Km + C} +k2 \cdot B & C(0) = 0 \\ & k1 = 3, k2 = 1, Vmax = 0.5, Km = 1 \end{align} \]

3. Add a measurement equation that states that you can measure the sum of the concentration of B and C

\[ \hat{y} = B + C \]

1.3 A receptor-substrate system

We have the system illustrated below, represented as an interaction graph, where all reactions are with mass action kinetics. R and Rp corresponds to a receptor which can be phosphorylated when stimulated with stimulation S. RS and RSp corresponds to a receptor substrate which can also be phosphorylated by the phosphorylated receptor Rp

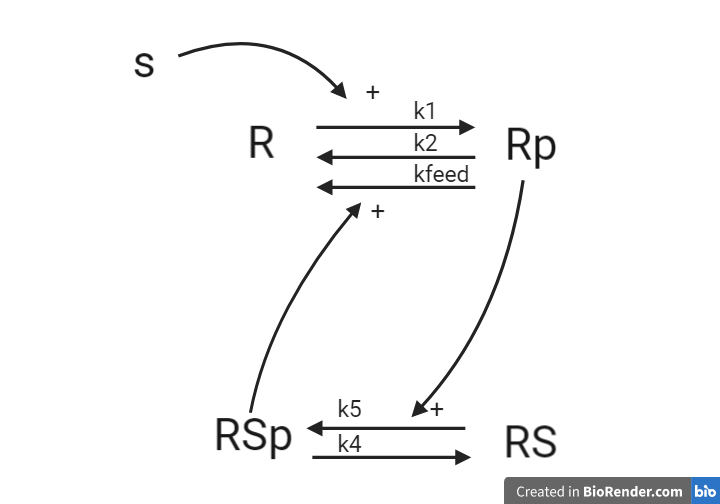
Questions

1. For the system, what are the reaction rates?
2. What are the ODEs? Reuse your reaction rates.
3. Define a measurement equation that corresponds to Rp

Answers

This system will later be implemented as a part of the computer exercise, you will get the answer to if the equations are corrected when you have implemented and simulated the model.

1.4 An alternative receptor-substrate system

In an alternative interpretation of the system from 1.2, the stimuli S is degraded over time by the phosphorylated receptor substrate RSp.

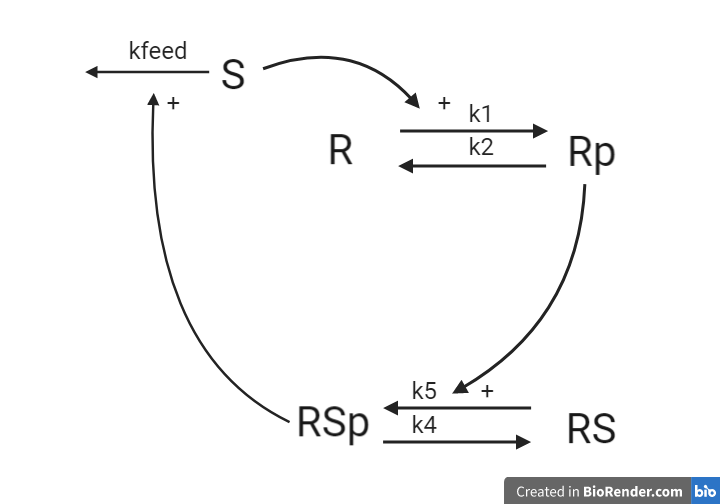
Questions

1. For the system, what are the reaction rates?
2. What are the ODEs? Reuse your reaction rates.

Answers

This system will later be implemented as a part of the computer exercise, you will get the answer to if the equations are corrected when you have implemented and simulated the model.

---

2. Formulating interaction graphs from equations

In this section you will practice creating interaction graphs from systems of ODEs.

2.1 A circular system

You have the following system of ODEs:

\[ \begin{align} &d/dt(A) = k1 - k2 \cdot A + k4 \cdot C\\ &d/dt(B) = \phantom{k1 - }\; k2 \cdot A - k3 \cdot B\\ &d/dt(C) = \phantom{k1 - }\; k3 \cdot B - k4 \cdot C\\ \\ &[k1, k2, k3, k4] = [1, 3, 2, 2] \\ &[A(0), B(0), C(0)] = [100, 0, 20] \end{align} \]

Questions

1. What are the reactions and reaction rates?
2. Given the system and the reactions, how could an interaction graph look? Mark each reaction with either the correspond parameter value or the reaction name in the graph.

Answers

1. Given the system of ODEs, what are the reactions and reaction rates?

We can see that \(A\) has an influx (which we refer to as \(v1\)), with the rate \(v1 = k1\). The reaction rate of \(v1\) does not appear in any other ODE, which means that we have a creation of \(A\) from "nothing". Thus, we have a reaction \(\varnothing \rightarrow A\) (or simply: \(\rightarrow A\)).

We can see that \(A\) has an outflux (which we refer to as \(v2\)), with the rate \(v2 = k2 \cdot A\). The reaction rate of \(v2\) also appears in the ODE for \(B\) as an influx. Thus, we have a reaction \(A \rightarrow B\).

We can also see that B has an outflux (which we refer to as \(v3\)), with the rate \(v3 = k3 \cdot B\). This reaction rate also appears as an influx in \(C\), thus we have a reaction \(B \rightarrow C\).

Finally, we can also see that \(C\) has an outflux (which we refer to as \(v4\)), with the rate \(v4 = k4 \cdot C\). This reaction rate also appears as an influx in \(A\), thus we have a reaction \(C \rightarrow A\).

In summary:

\[ \begin{align} \varnothing \rightarrow A & : \quad v1 = k1\\ A \rightarrow B & : \quad v2 = k2 \cdot A\\ B \rightarrow C & : \quad v3 = k3 \cdot B& \\ C \rightarrow A & : \quad v4 = k4 \cdot C \end{align} \]

2. Given the system and the reactions, how could an interaction graph look?

The interaction graph could look something like the graph below. Here, we marked each reaction with the name of the reaction rates we used in the previous question.

2.2 A system with both creation and degradation.

You have the following system of ODEs:

\[ \begin{align} &d/dt(A) = k1 \cdot C - k2 \cdot A\\ &d/dt(B) = \phantom{k1 \cdot C - }\; k2 \cdot A - k3 \cdot B\\ &d/dt(C) = \phantom{k1 \cdot C - }\; k3 \cdot B - k4 \cdot C\\ \\ &[k1, k2, k3, k4] = [2, 8, 1, 1] \\ &[A(0), B(0), C(0)] = [0, 0, 0] \end{align} \]

Questions

1. Given the system of ODEs, what are the reactions?
2. Given the system and the reactions, how could an interaction graph look? Mark each reaction with either the correspond parameter value or the reaction name in the graph.

Answers

1. Given the system of ODEs, what are the reactions?

We can see that \(A\) has an influx (which we refer to as \(v1\)), with the rate \(v1 = k1 \cdot C\). The reaction rate of \(v1\) does not appear in any other ODE, which means that we have a creation of \(A\) from "nothing". The creation of \(A\) is influenced by \(C\). Thus, we have a reaction \(\varnothing \rightarrow A\) (or simply \(\rightarrow A\)).

We can see that \(A\) has an outflux (which we refer to as \(v2\)), with the rate \(v2 = k2 \cdot A\). The reaction rate of \(v2\) also appears in the ODE for \(B\) as an influx. Thus, we have a reaction \(A \rightarrow B\).

We can also see that B has an outflux (which we refer to as \(v3\)), with the rate \(v3 = k3 \cdot B\). This reaction rate also appears as an influx in \(C\), thus we have a reaction \(B \rightarrow C\).

Finally, we can also see that \(C\) has an outflux (which we refer to as \(v4\)), with the rate \(v4 = k4 \cdot C\). This reaction rate does not appear in any other ODEs, which means that we have a degradation of \(C\) into "nothing". Thus we have a reaction \(C \rightarrow \varnothing\) (or simply \(C \rightarrow\)).

In summary:

\[ \begin{align} \varnothing \rightarrow A & : \quad v1 = k1 \cdot C\\ A \rightarrow B & : \quad v2 = k2 \cdot A\\ B \rightarrow C & : \quad v3 = k3 \cdot B& \\ C \rightarrow \varnothing & : \quad v4 = k4 \cdot C \end{align} \]

2. Given the system and the reactions, how could an interaction graph look?

2.3 A more complex system.

You have the following system of ODEs:

\[ \begin{align} &d/dt(A) = - k1 \cdot A + k2 \cdot B \cdot E\\ &d/dt(B) = \phantom{-} k1 \cdot A - k2 \cdot B \cdot E\\ &d/dt(C) = - k3 \cdot B \cdot C + k4 \cdot D \cdot G\\ &d/dt(D) = \phantom{-} k3 \cdot B \cdot C - k4 \cdot D \cdot G + k9 \cdot H\\ &d/dt(E) = - k5 \cdot E \cdot D + Vmax \frac{F}{Km + F}\\ &d/dt(F) = \phantom{-} k5 \cdot E \cdot D - Vmax \frac{F}{Km + F}\\ &d/dt(G) = - k7 \cdot G \cdot F + k8 \cdot H\\ &d/dt(H) = \phantom{-} k7 \cdot G \cdot F - k8 \cdot H - k9 \cdot H\\ \\ &[k1, k2, k3, k4, k5, Vmax, Km, k7, k8, k9] = [2, 8, 1, 1, 10, 1, 5, 6, 9, 3] \\ &[A(0), B(0), C(0), D(0), E(0), F(0), G(0), H(0)] = [100, 0, 100, 0, 100, 0, 100, 0] \end{align} \]

Questions

1. Given the system of ODEs, what are the reactions?
2. Given the system and the reactions, how could an interaction graph look? Mark each reaction with either the correspond parameter value or the reaction name in the graph.

Answers

1. Given the system of ODEs, what are the reactions?

\(A\) has an outflux (which we refer to as \(v1\)), with the rate \(v1 = k1 \cdot A\). The reaction rate of \(v1\) also appear in the ODE for \(B\) as an influx. Thus, we have a reaction \(A \rightarrow B\).

\(A\) also has an influx (which we refer to as \(v2\)), with the rate \(v2 = k2 \cdot B \cdot E\). The reaction rate of \(v2\) also appears in the ODE for \(B\) as an outflux. Thus, we have a reaction \(B \rightarrow A\).

\(C\) has an outflux (which we refer to as \(v3\)), with the rate \(v3 = k3 \cdot C \cdot B\). The reaction rate of \(v3\) also appear in the ODE for \(D\) as an influx. Thus, we have a reaction \(C \rightarrow D\).

\(C\) also has an influx (which we refer to as \(v4\)), with the rate \(v4 = k4 \cdot D \cdot G\). The reaction rate of \(v4\) also appears in the ODE for \(D\) as an outflux. Thus, we have a reaction \(D \rightarrow C\).

\(E\) has an outflux (which we refer to as \(v5\)), with the rate \(v5 = k5 \cdot E \cdot D\). The reaction rate of \(v5\) also appear in the ODE for \(F\) as an influx. Thus, we have a reaction \(E \rightarrow F\).

\(E\) also has an influx (which we refer to as \(v6\)), with the rate \(v6 = Vmax \frac{F}{Km + F}\). The reaction rate of \(v6\) also appears in the ODE for \(F\) as an outflux. Thus, we have a reaction \(F \rightarrow E\).

\(G\) has an outflux (which we refer to as \(v7\)), with the rate \(v7 = k7 \cdot G \cdot F\). The reaction rate of \(v3\) also appear in the ODE for \(H\) as an influx. Thus, we have a reaction \(G \rightarrow H\).

\(G\) also has an influx (which we refer to as \(v8\)), with the rate \(v8 = k8 \cdot H\). The reaction rate of \(v8\) also appears in the ODE for \(H\) as an outflux. Thus, we have a reaction \(H \rightarrow G\).

Finally, \(H\) has an outflux (which we refer to as \(v9\)), with the rate \(v9 = k9 \cdot H\). The reaction rate of \(v9\) also appear in the ODE for \(D\) as an influx. Thus, we have a reaction \(H \rightarrow D\).

In summary:

\[ \begin{align} A \rightarrow B & : \quad v1 = k1 \cdot A\\ B \rightarrow A & : \quad v2 = k2 \cdot B \cdot E \\ C \rightarrow D & : \quad v3 = k3 \cdot C \cdot B\\ D \rightarrow C & : \quad v4 = k4 \cdot D \cdot G\\ E \rightarrow F & : \quad v5 = k5 \cdot E \cdot D\\ F \rightarrow E & : \quad v6 = Vmax \frac{F}{Km + F}\\ G \rightarrow H & : \quad v7 = k7 \cdot G \cdot F\\ H \rightarrow G & : \quad v8 = k8 \cdot H\\ H \rightarrow D & : \quad v9 = k9 \cdot H\\ \end{align} \]

2. Given the system and the reactions, how could an interaction graph look?

---

3. Additional exercises

This section contains additional exercises that can be done for more practice at formulating models, and could be useful when e.g. preparing for the dugga.

3.1

Consider the following model

\[ \begin{align} & [ \dot{A}] = -k1[A] + k2[B] & [A](0) = 1 && \hat{y}=ky[A] \\ & [ \dot{B}] = -k2[B] + k1[A] & [B](0) = 1 && \end{align} \]

Questions

1. List all model states
2. List all model parameters
3. List all reaction rates
4. What can be measured? Explain in words.

Answers

1. List all model states

\([A]\), \([B]\)

Note that the brackets [] denotes that the states corresponds to a concentration, and are required to give for a correct answer.

2. List all model parameters

\(k1\), \(k2\), \(ky\).

The initial values (\([A](0)\), \([B](0)\)) are sometimes also considered as parameters.

3. List all reaction rates

\(k1[A]\), and \(k2[B]\)

4. What can be measured? Explain in words.

The measurement equation, \(\hat{y} = ky[A]\), shows that we can measure something that is proportional the concentration of A.

3.2

Consider the following model

\[ \begin{align} & [ \dot{A}] = -k1[A] + k3[C] & [A](0) = 1 \\ & [ \dot{B}] = -k2[B] + k1[A] & [B](0) = 0 \\ & [ \dot{C}] = -k3[C] + k2[B] & [C](0) = 0 \end{align} \]

Questions

1. Which are the reactions?
2. Choose one of the reactions and change the kinetics so that the reaction rate is saturated and give the new equations

Answers

1. Which are the reactions

\[ \begin{align} & A \rightarrow B\\ & B\rightarrow C \\ & C\rightarrow A \end{align} \]

2. Choose one of the reactions and change the kinetics so that the reaction rate is saturated and give the new equations

Lets update the reaction \(A \rightarrow B\) so that is is saturated with respect to A:

The new saturated reaction rate is now \(Vmax \cdot [A] / (Km + [A])\). Now we need to update the ODEs for \([A]\) and \([B]\):

\[ \begin{align} & [ \dot{A}] = -Vmax\cdot [A] / (Km + [A]) + k3[C] \\ & [ \dot{B}] = -k2[B] + Vmax\cdot [A] / (Km + [A]) \end{align} \]

3.3

Take the role as a systems biologist working in a project together with an experimental collaborator. Your collaborator can indirectly measure the concentration of insulin receptors at the surface of fat cells, i.e. all insulin receptors that are located in the plasma membrane. She is interested in how fat cells respond to the input insulin. She already has a hypothesis for key interactions of the underlying biological system, and ha made a drawing that shows this hypothesis (Figure 1). She thinks that the reaction where the insulin receptor recirculates from inside the cell to the plasma membrane is saturated so that it has a maximum rate. Now it is your role to interpret the drawing and formalize into equations.

Figure 1: The insulin receptor is located in the plasma membrane were insulin binds to the insulin receptor and forms a complex. This complex is either 1) internalized into the fat cell where insulin is released before the receptor recirculates to the plasma membrane or 2) resolved so that insulin is released and the insulin receptor is free to bind another insulin molecule.

Questions

Use the drawing above as the interaction graph for the model. Formulate the corresponding system of ordinary differential equations! Feel free to make assumptions, and include these assumptions in your answer. Introduce parameters with values of your choice. The result should be a complete model that can be simulated.

Suggested answer

1. Identify model states:

\[ \begin{align} &x1 = InsulinReceptor_{plasmamembrane} \\ &x2 = InsulinReceptor^{insulin}_{plasmamembrane} \\ &x3 = InsulinReceptor^{insulin}_{internalized} \\ &x4 = InsulinReceptor_{internalized} \end{align} \]

2. Define the reaction rates

Let us assume mass-action kinetics for all reactions except the saturated recirculation reaction (v5). Let us also assume that Insulin is the input u = Insulin.

\[ \begin{align} &v1 = k1 \cdot x1 \cdot u \\ &v2 = k2 \cdot x2 \\ &v3 = k3 \cdot x2 \\ &v4 = k4 \cdot x3 \\ &v5 = (Vmax \cdot x4)/(Km + x4) \end{align} \]

where

\[ \begin{align} &v1: \quad x1 \rightarrow x2 \\ &v2: \quad x2 \rightarrow x1 \\ &v3: \quad x2 \rightarrow x3 \\ &v4: \quad x3 \rightarrow x4 \\ &v5: \quad x4 \rightarrow x1 \end{align} \]

3. Formulate ODEs:

\[ \begin{align} &d/dt(x1) = −v1 + v2 + v5 \\ &d/dt(x2) = \phantom{-} v1 − v2 − v3 \\ &d/dt(x3) = \phantom{-} v3 − v4 \\ &d/dt(x4) = \phantom{-} v4 − v5 \end{align} \]

4. Define a measurement equation

Let us assume that we can measure something proportional to the sum of x1 and x2 since these states represent receptors in the plasma membrane.

\[ \hat{y} = ky \cdot (x1 + x2) \]

5. Define parameters and initial conditions, and their values:

\[ \begin{align} &[k1, k2, k3, k4, Vmax, Km, ky] = [3, 1, 2, 1, 1, 3, 0.5] \\ &[x1(0), x2(0), x3(0), x4(0)] = [10, 0, 10, 0] \end{align} \]

All parameter values are made up. We also assume a value for the input strength: \(u = 100\).

All of these values are needed to simulate the model.

Give the full system of ODEs:

\[ \begin{align} &d/dt(x1) = −v1 + v2 + v5 \\ &d/dt(x2) = v1 − v2 − v3 \\ &d/dt(x3) = v3 − v4 \\ &d/dt(x4) = v4 − v5 \\ \\ &v1: \quad x1 \rightarrow x2 \\ &v2: \quad x2 \rightarrow x1 \\ &v3: \quad x2 \rightarrow x3 \\ &v4: \quad x3 \rightarrow x4 \\ &v5: \quad x4 \rightarrow x1 \\ \\ &\hat{y} = ky \cdot (x1 + x2) \\ \\ &[x1(0), x2(0), x3(0), x4(0)] = [10, 0, 10, 0] \\ \\ &[k1, k2, k3, k4, Vmax, Km, ky] = [3, 1, 2, 1, 1, 3, 0.5] \\ & u = 10 \end{align} \]

3.4

Consider the following reactions

\[ \begin{align} & \quad A \rightarrow B \\ & \quad A \rightarrow \varnothing \\ & \quad B \rightarrow \varnothing \\ \end{align} \]

Questions

1. Write down the differential equations that corresponds to these reactions. Assume mass action kinetics. Introduce parameters and initial conditions with values of your choice.
2. Add a measurement equation that states that you can measure something that is proportional to the rate of the reaction \(A \rightarrow B\).

Answers

1. Write down the differential equations that corresponds to these reactions

\[ \begin{align} & [ \dot{A}] = - k1[A] -k2[A] & [A](0) = 1 \\ & [ \dot{B}] = \phantom{-} k1[A] - k3[B] & [B](0) = 2 \\ & k1 = 3, k2 = 1, k3 = 0.1 \end{align} \]

2. Add a measurement equation that states that you can measure something that is proportional to the rate of the reaction \(A \rightarrow B\)

\[ \hat{y} = ky \cdot k1[A] \]

3.5

Consider the following model

\[ \begin{align} & [ \dot{A}] = -k1[A][B] - k2[A] + u & [A](0) = 1 \\ & [ \dot{B}] = -k1[A][B] & [B](0) = 0 \\ & [ \dot{C}] = k2[A] & [C](0) = 0 \end{align} \]

Question

1. Which are the reactions?

Answers

1. Which are the reactions

\[ \begin{align} & A + B \rightarrow \varnothing\\ & A \rightarrow C \\ & \varnothing \rightarrow A \end{align} \]

3.6

Consider the following model

\[ \begin{align} & [ \dot{A}] = - k1[A]\\ & [ \dot{B}] = \phantom{-} k1[A] - k2 \cdot [B]\\ & \hat{y} = ky \cdot [B]\\ &[A](0) = 1 \\ &[B](0) = 0.5 \\ &k1 = 1, k2 = 3, ky = 2 \end{align} \]

Question

1. What are the underlying reactions?
2. Make the reaction \(A \rightarrow B\) reversible, update the equations affected.
3. What is the simulated measurement at t=0?
4. What is the value of \([B]\) at time t = 0.1, if you take one step with the Euler forward method (use the original equations)? Note: only do this if you know the Euler forward method already.
5. Update the measurement equation to be saturated with respect to \([B]\)

Answers

1. Which are the underlying reactions?

\[ \begin{align} & A \rightarrow B\\ & B \rightarrow \varnothing \\ \end{align} \]

2. Make the reaction \(A \rightarrow B\) reversible, update the equations affected.

Change \(k1[A]\) to \(k1f \cdot [A] - k1b \cdot [B]\). Replace the parameter \(k1\) with \(k1f\) and \(k1b\). Now, update the ODEs for [A] and [B]:

\[\begin{align} & [ \dot{A}] = - k1f \cdot [A] + k1b \cdot [B]\\ & [ \dot{B}] = \phantom{-} k1 \cdot [A] - k1b \cdot [B] - k2 \cdot [B]\\ &k1f = 2, k1b = 0.5 \end{align}\]

3. What is the simulated measurement at t=0?

\[ \hat{y}(0) = ky \cdot [B](0) = 2 \cdot 0.5 = 1 \]

4. What is the value of \([B]\) at time t = 0.1, if you take one step with the Euler forward method (use the original equations)?

\[ [B](0.1) = [B](0) + 0.1 \cdot d/dt([B]) = 0.5 + 0.1 \cdot (1 \cdot 1 - 3 \cdot 0.5) = 0.5 + 0.1 \cdot (-0.5) = 0.45 \]

5. Update the measurement equation to be saturated with respect to \([B]\)

Update the equation and introduce new parameters \(Vmax2\) and \(Km2\) with arbitrary values.

\[ \begin{align} &\hat{y}(0) = Vmax2 \cdot [B]/(Km2 + [B])\\ &Vmax2 = 3.5, Km2 = 55 \\ \end{align} \]

3.7

Consider the following reactions

\[ \begin{align} & X1 \rightarrow X3\\ & X3 \leftrightarrow X1 + X2 \\ \end{align} \]

and assume that the model states correspond to concentrations.

Question

1. Assume that the first reaction is described by Michaelis-Menten kinetics, and the second by mass action. What are the differential equations?
2. Assume that you can measure the sum of the concentrations of \(X1\) and \(X2\), and that everything is located in the \(X1\) state at time 0. Write the initial conditions and the measurement equation.
3. What are the states in the model?
4. What are the parameters?
5. Assume that \(X2\) is controlled by the user, i.e. it is an input. What would change?

Answers

1. Assume that the first reaction is described by Michaelis-Menten kinetics, and the second by mass action. What are the differential equations?

\[ \begin{align} & v1 = Vmax \cdot [X1]/(Km + [X1])\\ & v2f = k2f \cdot [X3] \\ & v2b = k2b \cdot [X1] \cdot [X2]\\ & v2 = v2f - v2b \\ & d/dt([X1]) = - v1 + v2 \\ & d/dt([X2]) = \phantom{-} v2 \\ & d/dt([X3]) = \phantom{-} v1 - v2\\ \end{align} \]

2. Assume that you can measure the sum of the concentrations of \(X1\) and \(X2\), and that everything is located in the \(X1\) state at time 0. Write the initial conditions and the measurement equation.

\[ \begin{align} & [X1](0) = 10 \\ & [X2](0) = 0 \\ & [X3](0) = 0 \end{align} \]

Note that the value of \(X1[0] = 10\) is arbitrarily selected, but that the values of \(X2[0]\) and \(X3[0]\) must be 0 since "everything is located in the \(X1\) state at time 0"

3. What are the states in the model?

\([X1]\), \([X2]\) and \([X3]\)

4. What are the parameters?

\(Vmax\), \(Km\), \(k2f\), \(k2b\). (note: no measurement parameters in this model)

5. Assume that \(X2\) is controlled by the user, i.e. it is an input. What would change?

You could write \(u = [X2]\), remove the differential equation for \(d/dt([X2])\), and replace \(v2b\) with \(v2b = k2b \cdot [X1] \cdot u\).

3.8

Consider the following model:

\[ \begin{align} & d/dt(x1) = -k1 \cdot x1 + Vmax \cdot x2/(Km + x2) \\ & d/dt(x2) = k1 \cdot x1 - Vmax \cdot x2/(Km + x2) - k3 \cdot x2 \\ & yhat = kmeas \cdot (x1 + x2) \end{align} \]

where \(x1 = [X1]\), and \(x2 = [X2]\).

Question

1. What are the underlying reactions making up the interaction graph of this model?
2. Assume that the \(k1\)-reaction is saturated. What changes?
3. Assume that on top of the change in 2), the original \(Vmax\)-reaction no longer is saturated. What happens?
4. Assume that on top of the change in 3), there appears a new reaction that creates \(x1\), with a constant rate k0. What changes?
5. Assume that on top of the change in 4), the \(k3\)-reaction is saturated with respect to \(x2\), and that it creates the substance \(X3\). What changes?
6. Assume that we obtain a new measurement that is proportional to the concentration of \(X3\). What changes?

Answers

1. What are the underlying reactions making up the interaction graph of this model?

\[ \begin{align} & R1: \quad X1 \rightarrow X2 \quad \text{(mass-action, constant k1)} \\ & R2: \quad X2 \rightarrow X1 \quad \text{(Michaelis-Menten, Vmax, Km)} \\ & R3: \quad X2 \rightarrow \varnothing \quad \text{(mass-action, constant k3)} \end{align} \]

Note that we here differentiate between the state \(x1\), and the protein/substance whose concentration \(x1\) is describing, \(X1\). This is the correct way to do things, but you would pass a dugga even if you write e.g. \(x1 \rightarrow x2\) as the first reaction.

2. Assume that the \(k1\)-reaction is saturated. What changes?

\[ \begin{align} &d/dt(x1) = -Vmax1 \cdot x1/(Km1 + x1) + Vmax \cdot x2/(Km + x2) \\ &d/dt(x2) = Vmax1 \cdot x1/(Km1 + x1) - Vmax \cdot x2/(Km + x2) - k3 \cdot x2 \end{align} \]

Note: if there would have been parameters defined (which there should be), these would have to be updated.

3. Assume that on top of the change in 2), the original \(Vmax\)-reaction no longer is saturated. What happens?

\[ \begin{align} &d/dt(x1) = -Vmax1 \cdot x1/(Km1 + x1) + k2 \cdot x2 \\ &d/dt(x2) = Vmax1 \cdot x1/(Km1 + x1) - k2 \cdot x2 - k3 \cdot x2 \end{align} \]

Note: if there would have been parameters defined (which there should be), these would have to be updated.

4. Assume that on top of the change in 3), there appears a new reaction that creates \(x1\), with a constant rate \(k0\). What changes?

\[ \begin{align} &d/dt(x1) = -Vmax1 \cdot x1/(Km1 + x1) + k2 \cdot x2 + k0 \\ &d/dt(x2) = Vmax1 \cdot x1/(Km1 + x1) - k2 \cdot x2 - k3 \cdot x2 \end{align} \]

Note: if there would have been parameters defined (which there should be), these would have to be updated.

Assume that on top of the change in 4), the \(k3\)-reaction is saturated with respect to \(x2\), and that it creates the substance \(X3\). What changes?

\[ \begin{align} &d/dt(x1) = -Vmax1 \cdot x1/(Km1 + x1) + k2 \cdot x2 + k0 \\ &d/dt(x2) = Vmax1 \cdot x1/(Km1 + x1) - k2 \cdot x2 - Vmax3 \cdot x2/(Km3 + x2) \\ &d/dt(x3) = Vmax3 \cdot x2/(Km3 + x2) \end{align} \]

where \(x3 = [X3]\).

Note: if there would have been parameters defined (which there should be), these would have to be updated.

Assume that we obtain a new measurement that is proportional to the concentration of \(X3\). What changes?

We get a new measurement equation \(\hat{y}2 = ky2 \cdot x3\)